QR Decomposition

QR 분해의 근본적인 이유는 무엇일까? 기존의 선형대수에 대한 글에서, 행렬은 하나의 공간을 매핑한다고 했다.

그리고 행렬 size가 정사각행렬이고, full rank일 때 n차원 공간을 매핑한다.

그런데 공간을 매핑하는데 있어, 굳이 orthogonal 할 필요는 없다.

즉, 직교하는 축으로 공간이 매핑될 필요는 없다.

하지만, 우리는 직교축에 익숙하다! 또한 다루기도 매우 쉽다!

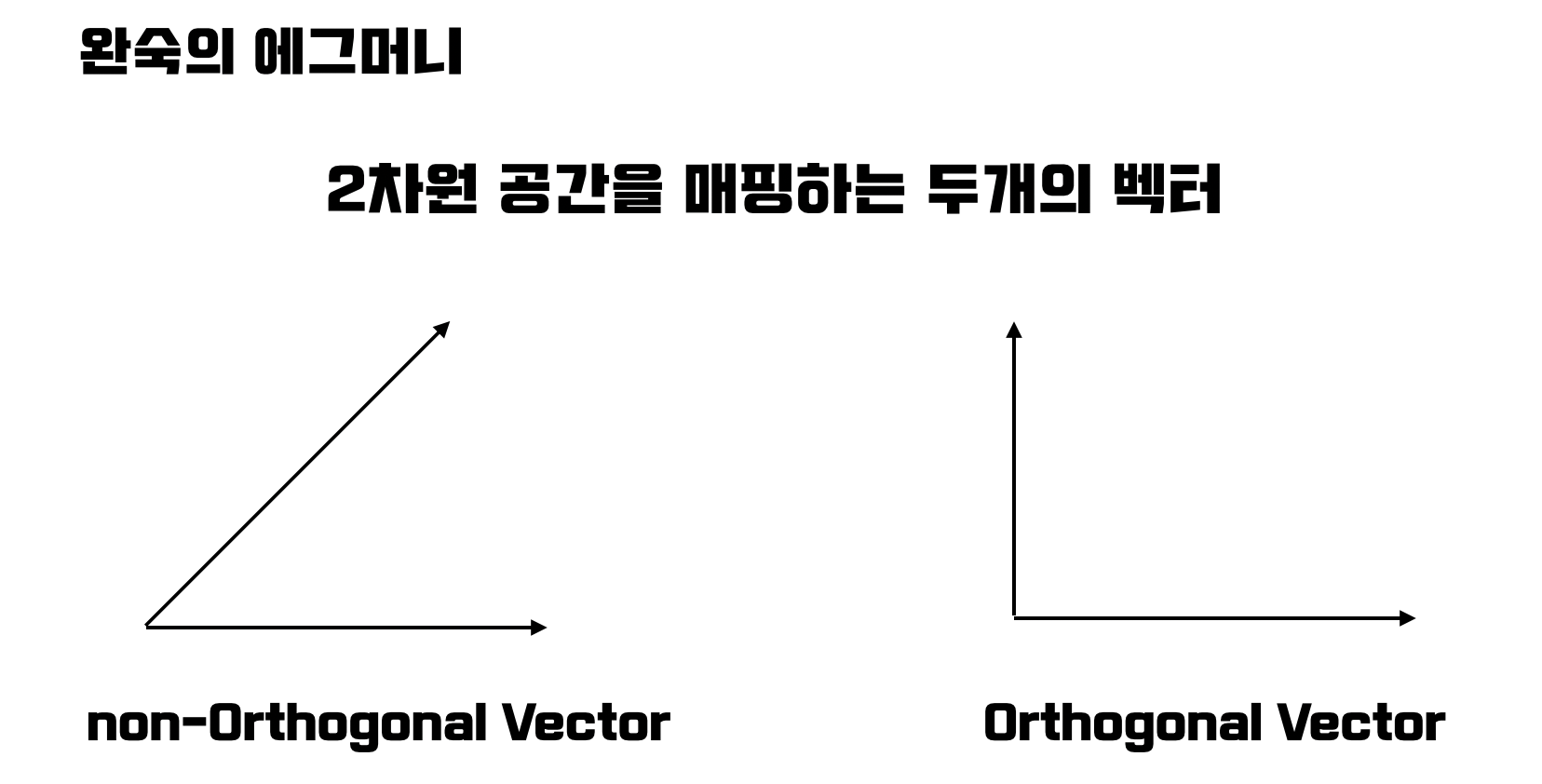따라서 우리는 특정 행렬이 Orthogonal 한 행렬로 나타내어 진다면 다루기 굉장히 수월할 것이다! 필요성이 생겼으니 만들어보자.

Assumption

A; =; [a_{1} \to a_{2} \to \dots a_{m} \to]; s i ze; =; n \times m

A 행렬의 모든 벡터는 선형 독립 이다.

Idea

2 차원 공간에서 먼저 생각해보자.

우리가 하고 싶은 것은, A 벡터를 Orthogonal 한 벡터로 변환시키는 것이다. 그전에, 어떤 직교행렬로 만들지에 대한 고민이 필요한데,

그러기 위해서는 기준이 필요하다. 그래서 우리는 직교행렬로 만들 첫번째 축(b1)을 a1 벡터로 선택할 것이다.

그렇다면, 우리는 b1에 직교하는 축, b2를 만들어야 하는데, 이녀석은 어떻게 정의할 수 있을까?

a2 벡터의 방향으로 부터, a1 벡터의 성분을 제거 해준다면 그 남은 벡터가 b2 벡터라 할 수 있을 것이다.

스크린샷 2019-05-04 오후 5 08 15

그 다음 3차원 벡터는,

a3 벡터에서, b1벡터의 성분을 빼고, b2벡터의 성분을 빼면 된다!

Process

이 과정을 수식화해보면, 첫번째 요소는,

o v erse t \to b_{1}; =; a_{1} \to

ha t b_{1} \to; =; \frac{a _{1} \to}{∣ a _{1} \to ∣}

두번째 요소는,

o v erse t \to b_{2}; =; a_{2} \to - (a_{2} \to^{T} \hat{b_{1} \to}) \hat{b_{1} \to}

세번째 요소는,

o v erse t \to b_{3}; =; a_{3} \to - (a_{3} \to^{T} \hat{b_{1} \to}) \hat{b_{1} \to} - (a_{3} \to^{T} \hat{b_{2} \to}) \hat{b_{2} \to}

i 번째 요소는,

o v erse t \to b_{i}; =; a_{i} \to - \sum_j = 1^{i - 1} (a_{i} \to^{T} \hat{b_{j} \to}) \hat{b_{j} \to}

Transform to Matrix form

행렬 A에 대해 정리하기 위해, a벡터에 대해 정리해보자.

o v erse t \to a_{i}; =; b_{i} \to + \sum_j = 1^{i - 1} (a_{i} \to^{T} \hat{b_{j} \to}) \hat{b_{j} \to}

여기서,

ha t b_{i} \to; =; \frac{b _{i} \to}{∣ b _{i} \to ∣}

이므로,

o v erse t \to a_{i}; =; ∣ b_{i} \to ∣ \hat{b_{i} \to} + \sum_j = 1^{i - 1} (a_{i} \to^{T} \hat{b_{j} \to}) \hat{b_{j} \to}

이 식을 A 식이라 하자.

여기서 양쪽에 b의 단위 벡터를 곱하자.

ha t b_{i} \to^{T} a_{i} \to; =; ∣ b_{i} \to ∣ \hat{b_{i} \to}^{T} \hat{b_{i} \to} + \sum_j = 1^{i - 1} (a_{i} \to^{T} \hat{b_{j} \to}) \hat{b_{i} \to}^{T} \hat{b_{j} \to}

이 때, Orthogonal vector의 특징으로 부터,

ha t b_{i} \to^{T} \hat{b_{j} \to}; =; {1, 0, i = j i \neq = j

시그마로 표시된 우측항은 0 이다.

또한, 그 왼쪽항도 1이 되어 b벡터의 크기만 남는다.

ha t b_{i} \to^{T} a_{i} \to; =; ∣ b_{i} \to ∣

여기서 왼쪽항을 전치행렬의 특징을 사용해서 뒤바꾸면,

o v erse t \to a_{i}^{T} \hat{b_{i} \to}; =; ∣ b_{i} \to ∣

이 결과를 A 식에 대입하면,

o v erse t \to a_{i}; =; ∣ b_{i} \to ∣ \hat{b_{i} \to} + \sum_j = 1^{i - 1} (a_{i} \to^{T} \hat{b_{j} \to}) \hat{b_{j} \to};; a_{i} \to; =; (a_{i} \to^{T} \hat{b_{i} \to}) \hat{b_{i} \to} + \sum_j = 1^{i - 1} (a_{i} \to^{T} \hat{b_{j} \to}) \hat{b_{j} \to};; a_{i} \to; =; \sum_j = 1^{i} (a_{i} \to^{T} \hat{b_{j} \to}) \hat{b_{j} \to}

여기서 괄호안을 전치행렬의 특징을 사용해서 뒤바꾸면,

o v erse t \to a_{i}; =; \sum_j = 1^{i} (\hat{b_{j} \to^{T}} a_{i} \to) \hat{b_{j} \to}

이제 행렬모양으로 바꿔보자.

A;=;\begin{bmatrix} \overset{\rightarrow}{a_1} & \overset{\rightarrow}{a_2} & \cdots & \overset{\rightarrow}{a_m}\\ \end{bmatrix}\\ ;\\ =\begin{bmatrix} \hat{\overset{\rightarrow}{b_1}} & \hat{\overset{\rightarrow}{b_2}} & \cdots & \hat{\overset{\rightarrow}{b_m}}\\ \end{bmatrix} \begin{bmatrix} {\hat{\overset{\rightarrow}{b_1}^T}\overset{\rightarrow}{a_1}} & {\hat{\overset{\rightarrow}{b_1}^T}\overset{\rightarrow}{a_2}} & \dots & \hat{\overset{\rightarrow}{b_1}^T}\overset{\rightarrow}{a_m}\\ 0 & {\hat{\overset{\rightarrow}{b_2}^T}\overset{\rightarrow}{a_2}} & \dots & \hat{\overset{\rightarrow}{b_1}^T}\overset{\rightarrow}{a_m} \\ \vdots & & \ddots & \vdots\\ 0 & 0 & \dots & \hat{\overset{\rightarrow}{b_m}^T}\overset{\rightarrow}{a_m}\\ \end{bmatrix}\\ ;\\ ;\\;\\ A;=QR;\\ ;\\ \[n\times m\];=;\[n\times m \];\times;\[m\times m\]

A가 정사각행렬일 때,

A; =; QR

A x \to; =; b \to; QR x \to; =; b \to; Q^{T} QR x \to; =; Q^{T} b \to; I R x \to; =; Q^{T} b \to; R x \to; =; Q^{T} b \to

orthogonal matrix의 특성에 따라 전치행렬을 곱하면 identity matrix가 나온다.

그리고 R 행렬은 upper triangle matrix 이다.

🥚

Explorer

Recent Notes

2024-10

Hessian Matrix

Jacobian Matrix

QR Decomposition

QR Decomposition

Assumption

Idea

Process

Transform to Matrix form

A가 정사각행렬일 때,

Graph View

Table of Contents

Backlinks