Intuition Concept

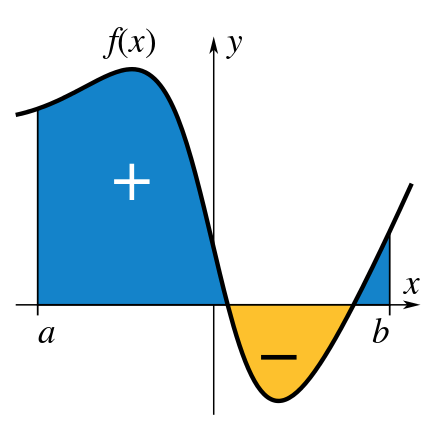이게 정적분이죠! 하지만 컴퓨터는 연속적인 값을 인식할 수 없기 때문에

(사실 점들의 집합이 선이긴 하죠) 이산적인 값에 대해서 이 값에 근사해야 합니다.

그 전에 이 정적분의 정의를 어떤 것에서 확장했었죠?

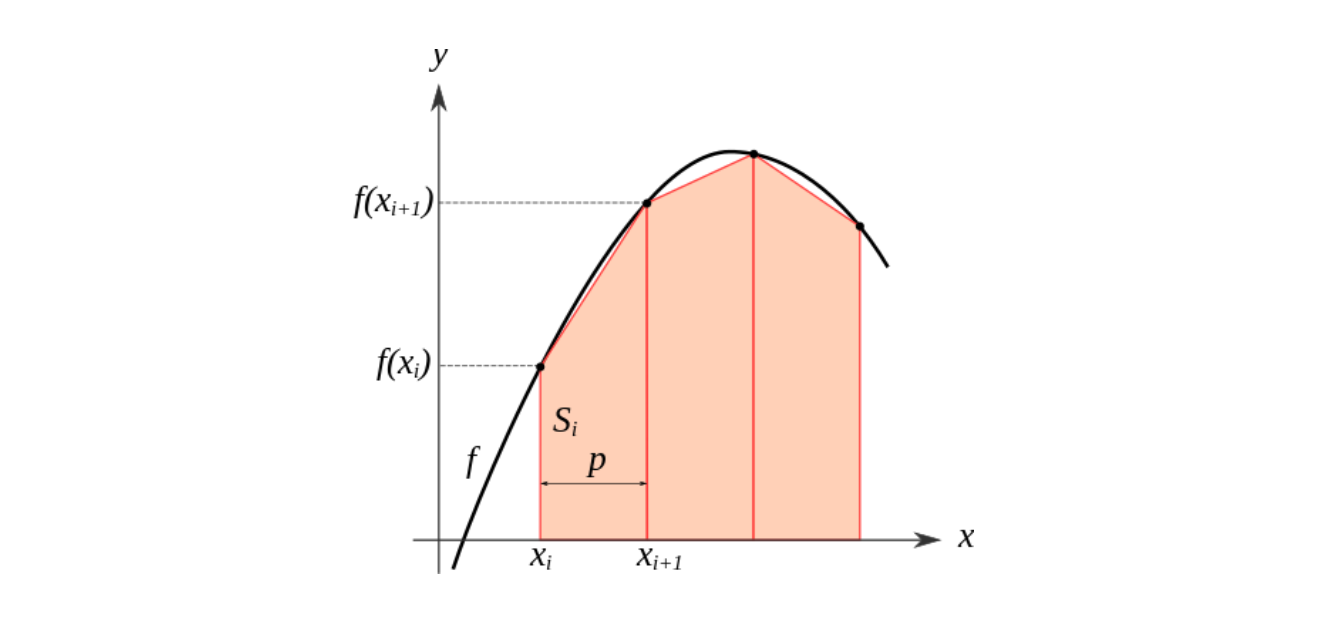
바로 구분구적법으로 나타냈었습니다.

고등학교 과정에서는 직사각형의 합의 형태로 나타내었지만 우리는 무한개의 사각형의 합으로 나타낼 수 없고 이산적 근사하는 방법을 Trapezoidal rule 이라 합니다.

1차식인 Trapezoidal rule이 가장 쉬우므로 이때의 근사식을 유도해보면,

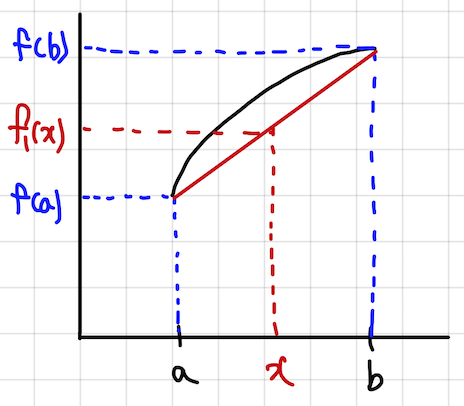
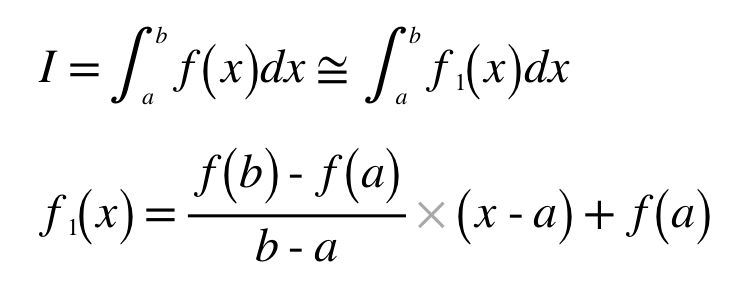
f1을 위의 식에 대입하면,

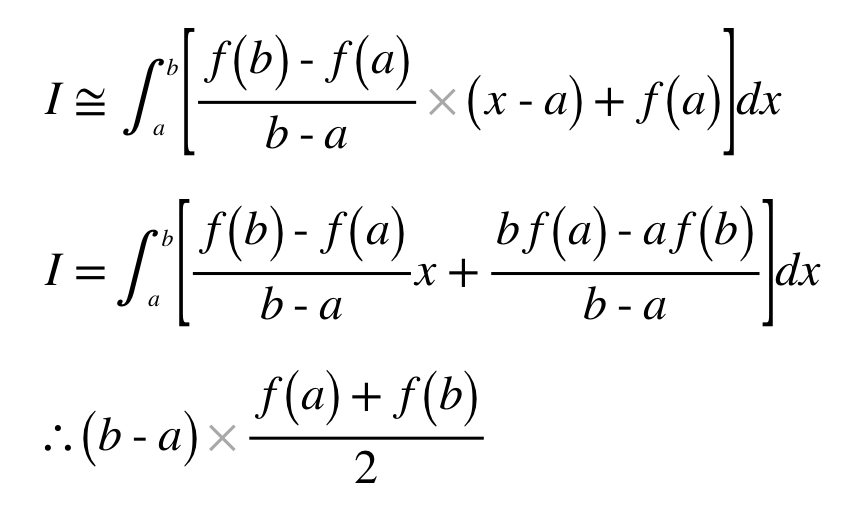n개의 사다리꼴을 모두 더하게 되면,

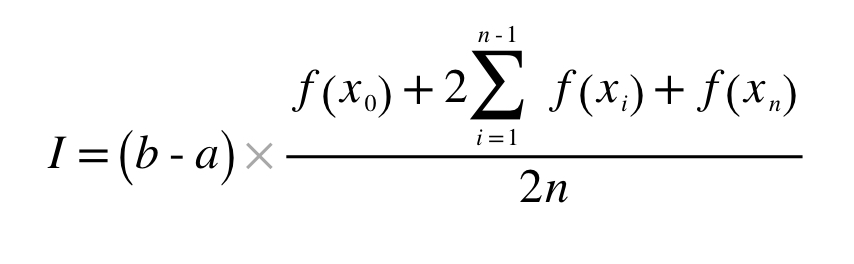
그런데 두 점을 굳이 직선으로 이을 필요는 없겠죠.

해당 부분을 대변할 수 있는 다른 곡선을 채택해서 그 식에 대해 적분을 해도 괜찮을 겁니다.

결국 이 방법들은 수치해석에서 뉴턴-코츠 법칙들의 경우들 입니다.

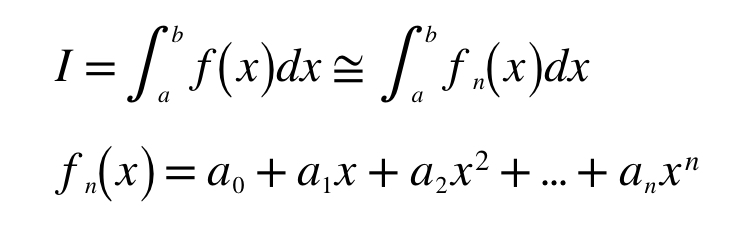
n차 다항식의 경우를 생각하면 이런식으로 됩니다.

두 점을 잇는다는 관점에서 이건 보간법에서 한 것과 사실 비슷해요.

어떤 차수의 다항식을 사용하느냐에 따라, quad, quadgk, quadl, triplequad, integral, integral2, …

이렇게 많은 방법이 존재합니다. 이 중 한가지만 살펴보면, quad함수는 Simpson’s rule을 따릅니다.

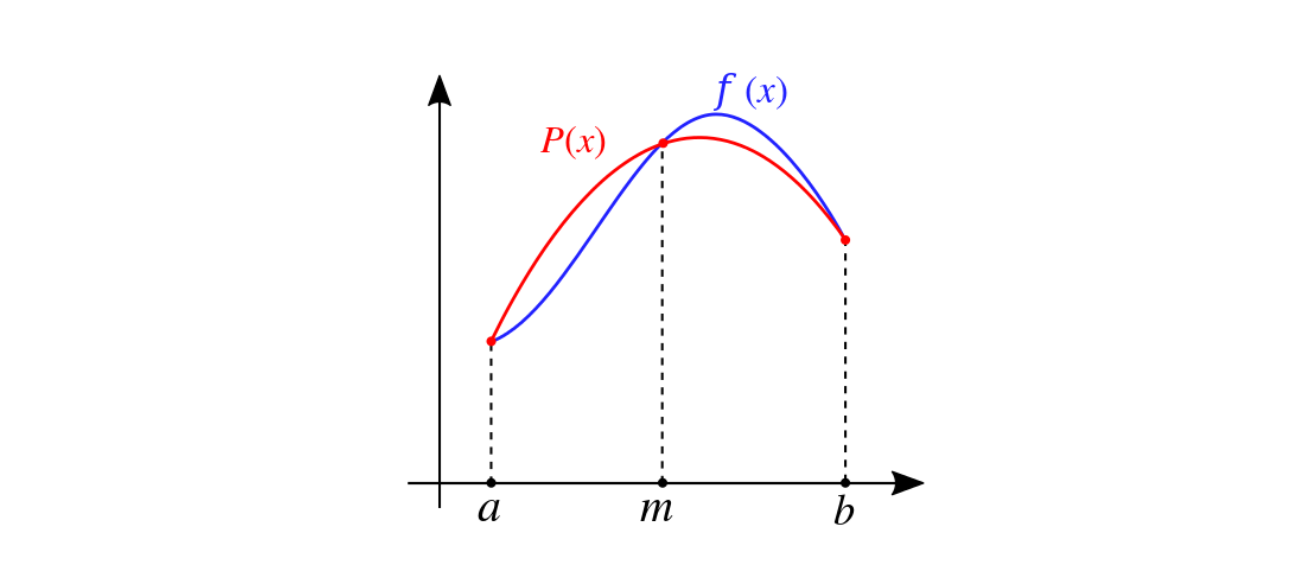
P(x)라는 2차방정식으로 f(x)의 근사값을 구하는 방법입니다.
자세한 내용은 하단 링크를 따라서 공부해보길 바랍니다.

Function

Trapezoidal rule 적분근삿값 = trapz(x_array, y_array)

입력변수는 array여야 합니다. 매트랩에서 함수란 결국 두 array간의 관계를 나타내는 것이기 때문입니다.

x, y array 의 길이는 같아야 합니다. 하지만 Simpson’s rule 을 사용하는 방법은,

Simpson's rule 적분근삿값 = quad(function, 시작값, 끝값)

함수를 따로 정해줄 필요 없이 입력변수로 받는다는 점에서 차이가 있습니다.

0 < x < 1 의 범위내에서 x^2의 적분값을 구해라.

Trapezoidal rule 를 만족하는 함수를 만들어보자.

function [I]=trapm(a,b,n,f) 
h=(b-a)/n; 
xp=linspace(a,b,n); 
yp=f(xp); 
sumf=0 for i=2:n     
	sumf=sumf+yp(i)+yp(i-1); 
end 
I=(h/2)*sumf;

Trapezoidal rule 의 최종 식을 그대로 옮겼다.

적분값을 구하기 위해서는 이 함수를 가져다 사용하면 된다.

f = @(x) x.^2; tramp_int_x = Trapm(0,1,100,f)

trapm_int_x =      0.3333

trapz 함수를 사용해보면,

f = @(x) x.^2; 
xp = linspace(0,1,100); 
yp = f(xp); 
trapz_int_x = trapz(xp, yp)

trapz_int_x =      
	0.3334

Simpson’s rule 도 사용해보자.

f = @(x) x.^2; 
simp_int_x = quad(f, 0, 1)

simp_int_x =     
	0.3333

Simpson’s rule 로도 같은 값을 얻을 수 있다.