Softmax Function

Logistic Regression 의 그래프

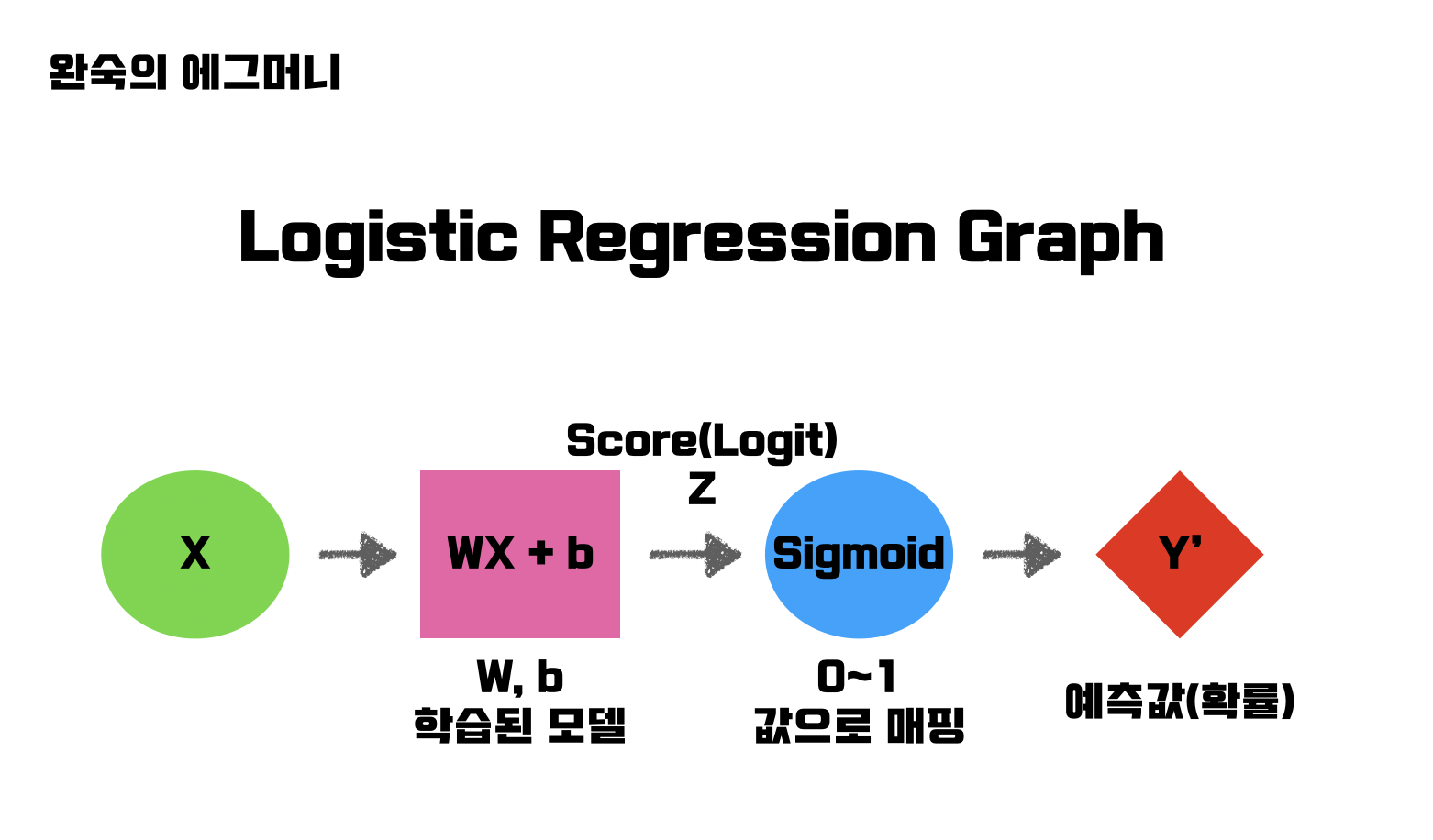함수를 통과하기 전의 값을 Score(Logit) 이라 부른다. 통과한 난 뒤의 값은 확률이다.

사실 이 작업은, 데이터를 그래프에 뿌려놨을 때, 두 가지 클래스로 구분할 수 있는 구분선 을 찾는 것과 같은 작업이다!!

0.5의 확률을 기준으로 두 클래스로 나누고 있으므로, 그 0.5를 만족하는 점들의 집합이 바로 구분선이다.

Softmax function

그렇다면 여러 개의 클래스를 분류해야 한다면 어떻게 해야할까?

위의 Logistic regression의 아이디어를 이용할 수 있는데, 만약 A, B, C 세 개의 클래스가 있다면

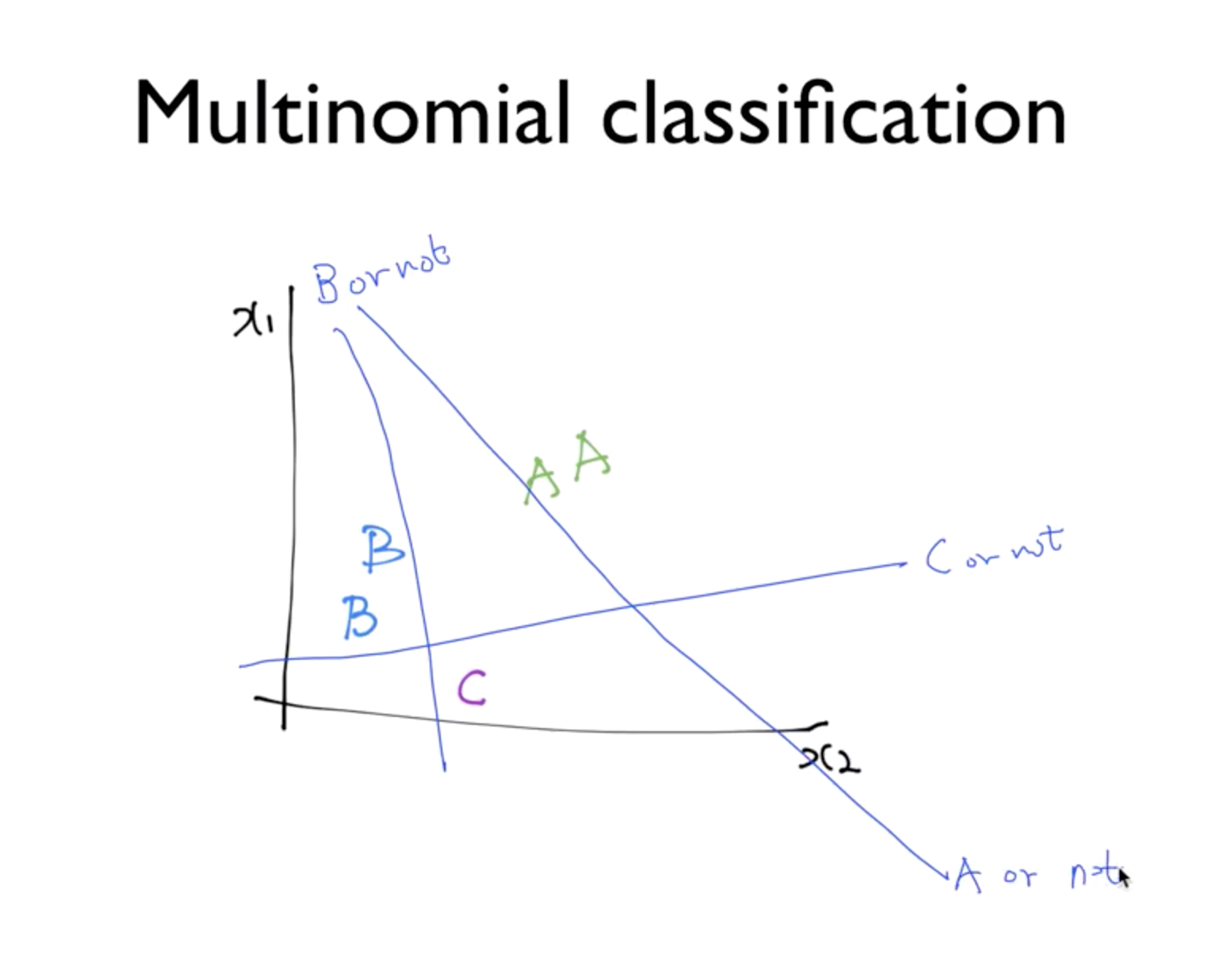
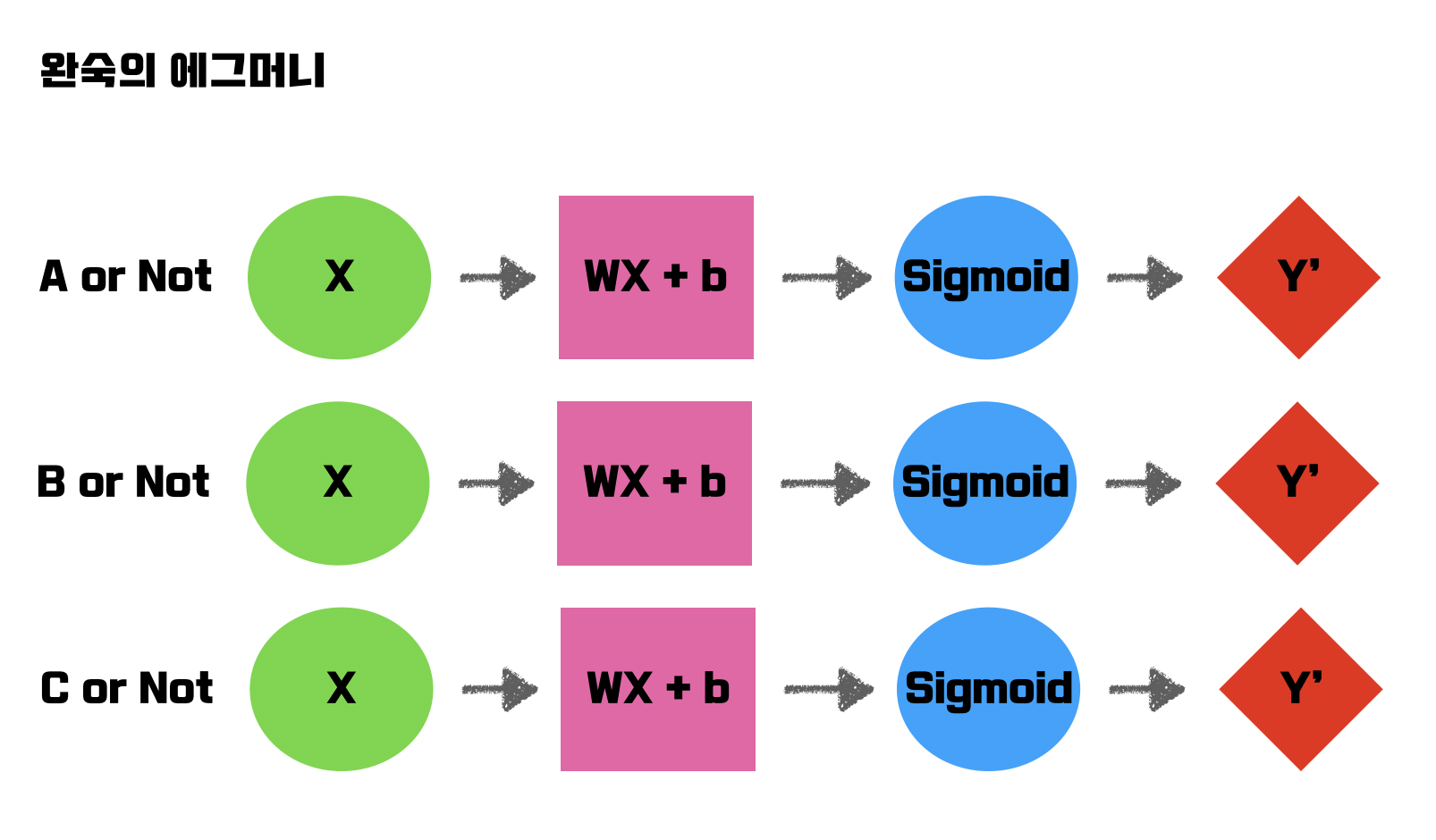세 개의 독립적인 logistic regression을 사용하면, 저렇게 3개의 선이 그어질 수 있다.

그리고 3개의 모델을 돌린 후 결과는, 해당 포인트의 점이 A, B, C 각각에 포함될 확률이 나올 것이다.

$$\begin{gathered} (w_1;w_2;w_3)\cdot \left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right);=;(x_1{w}_1+x_2{w}_2+x_3{w}_3); \\ ; \\ (w_1;w_2;w_3)\cdot \left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right);=;(x_1{w}_1+x_2{w}_2+x_3{w}_3); \\ ; \\ (w_1;w_2;w_3)\cdot \left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right);=;(x_1{w}_1+x_2{w}_2+x_3{w}_3); \\ ; \end{gathered}$$

그런데 이걸 구현하려고 보니 너무 복잡하고 구현하기 힘들어 보인다. 그래서 행렬을 사용한다.

\\begin{pmatrix} w\_{A1} & w\_{A2} & w\_{A3} \\ w\_{B1} & w\_{B2} & w\_{B3} \\ w\_{C1} & w\_{C2} & w\_{C3}\end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3\end{pmatrix};=;\begin{pmatrix} x_1w\_{A1}+x_2w\_{A2}+x_3w\_{A3} \\ x_1w\_{B1}+x_2w\_{B2}+x_3w\_{B3} \\ x_1w\_{C1}+x_2w\_{C2}+x_3w\_{C3}\end{pmatrix}=\begin{pmatrix} \hat{y_A} \\ \hat{y_B} \\ \hat{y_C}\end{pmatrix}

이렇게 벡터로 한번에 처리가 가능하다!

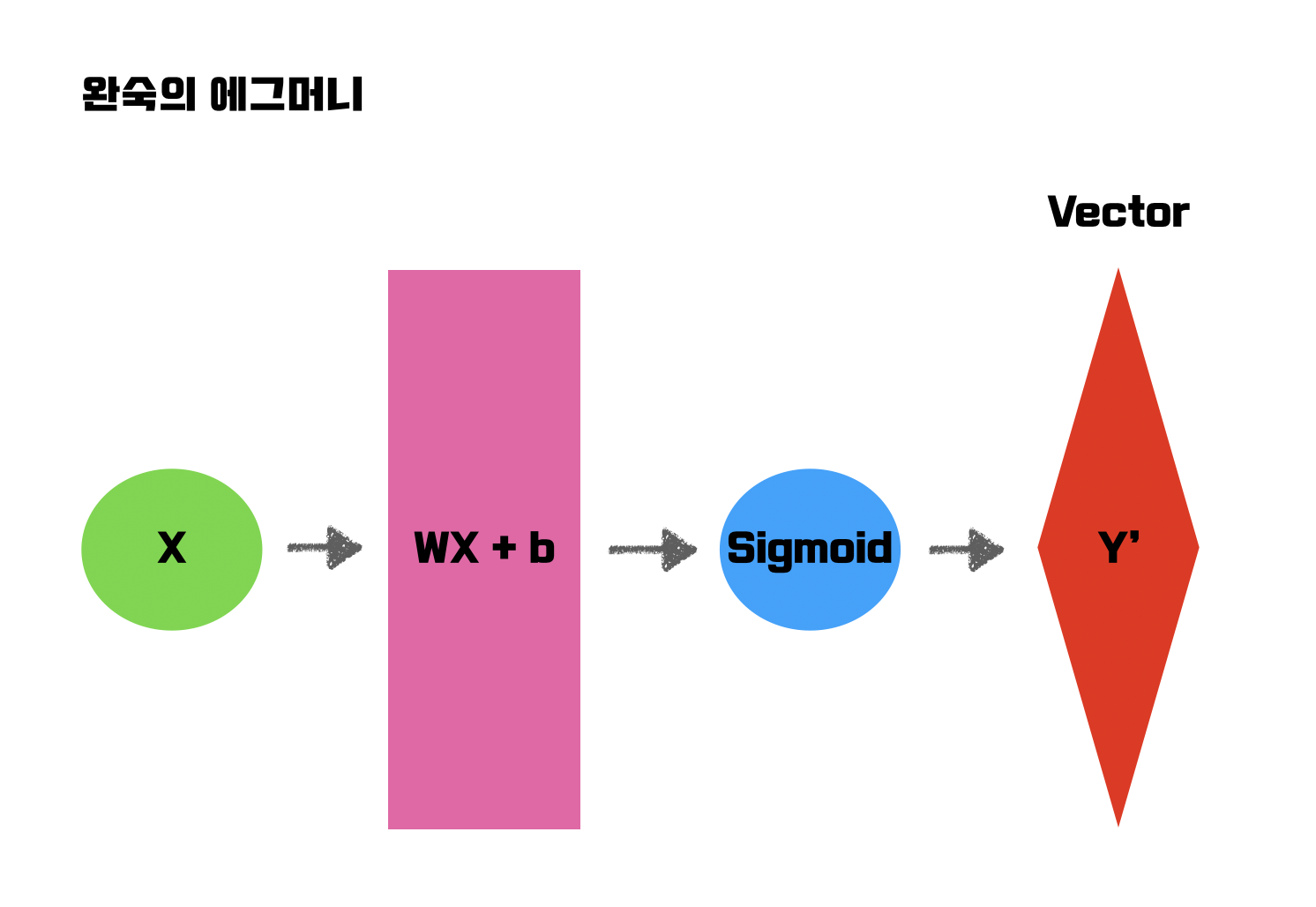Z 벡터를 sigmoid에 넣어 확률 벡터를 나오게하면 된다.

이걸 가능하게 하는 것이 Softmax Function 이다.

회귀로 돌린 Z값을 넣게 되면, 확률로 매핑시켜 준다.

Cost Function

그럼 이걸 학습 시키기 위해 Cost Function을 정의해야 한다.

Logistic 같은 경우 cost function을 미분한 것을 gradient descent 했지만

이번에는 조금 다르다. Cross Entropy를 사용한다. 밑에서 왜 이 지표가 맞는지 알아보자.

Cross Entropy

$$-\sum _i{y}_{i}log(\widehat{y_i})=\sum _i{y}_i\text{*}-log(\widehat{y_i})$$

이 때, -log 함수는 y hat의 값이 01의 확률 값이므로 무한대0 값을 갖는다.

예를 들어 생각해보자. 두 가지 레이블을 가질 수 있고,

순서대로 A 클래스, B 클래스인지 나타내는 Array 형태로 답안이 제출된다 하자.

실제값(y) = [0 1] # B클래스가 답임
예측값1(y_hat) = [0 1] # B클래스일 확률이 100%라고 예측
예측값2(y_hat) = [1 0] # A클래스일 확률이 100%라고 예측

우리가 하고 싶은 것은, 맞았을 때는 cost function의 값이 작게, 틀렸을 때는 cost function의 값이 크게 나오게 하는 것이다. 그리고나서 이 함수를 최소화하는 방향의 모델을 만드는 것이 목적이다.

그렇다면, Cross Entropy가 내가 생각하는 이 과정이 맞는지 생각해보자.

예측값 1의 경우,

\\begin{bmatrix} 0 \\ 1 \end{bmatrix} \cdot -log\begin{bmatrix} 0 \\ 1 \end{bmatrix};=;\begin{bmatrix} 0 \\ 1 \end{bmatrix}\cdot\begin{bmatrix} ∞ \\ 0 \end{bmatrix};=;0+0;=;0

예측값이 맞았을 때, 값이 0이 뜬다. 예측값 2의 경우,

\\begin{bmatrix} 0 \\ 1 \end{bmatrix} \cdot -log\begin{bmatrix} 1 \\ 0 \end{bmatrix};=;\begin{bmatrix} 0 \\ 1 \end{bmatrix}\cdot\begin{bmatrix} 0 \\ ∞ \end{bmatrix};=;0+∞;=;∞

값이 커진다.

즉, 틀린 예측에 대해 아주 큰 값의 penelty 를 주고 있음을 알 수 있다.

Logistic Regression & Cross Entropy

두 개의 레이블이 있다고 생각할 때, Cross Entropy는 다음과 같다.

$$-\sum _i{y}_{i}log(\widehat{y_i});=;-y_{1}log(\widehat{y_1})-y_{2}log(\widehat{y_2})$$

그런데, 로지스틱 회귀는 레이블이 2개가 있고, 또 하나가 결정될 때, 반대는 1에서 뺀 값이다.

$$\begin{gathered} y_2;=;1-y_1; \\ \widehat{y_2};=;1-\widehat{y_1} \end{gathered}$$ $$-y_{1}log(\widehat{y_1})-(1-y_1)log(1-\widehat{y_1})$$

위 식은 logistic 회귀에서 비용함수이다.

Reference

• Softmax function - Wikipedia