Category Theory Prolog

수학에서의 범주론에 대해 알아보자. 왜 Monad는 이런 형태가 된 것인가?

Monad, Category Theory

• Monad라는 단어는 프로그래밍에서 태동된 단어가 아니다.
• 수학에서의 범주론에서 유래된 단어이다.
• 그렇기 때문에 프로그래밍의 Monad는 수학의 Monad와 밀접한 관계가 있다.
• 프로그래밍에서의 Monad는 Type Category Monad라고하는 특별한 모나드에 불과하다.
• 수학적 개념을 알아야 프로그래밍의 모나드를 배울 수 있는 것은 아니다.

왜 알면 좋은가 1

• 그럼 왜 배우는가?
• 프로그래밍 언어의 모나드 개념을 통합시켜주기 때문이다.
• 상위 개념을 안다면, 하위 개념은 쉽게 이해되기 마련이다.
• 모나드라는 아이디어를 프로그래밍 언어에서 구현하는 방식은 여러가지가 있다.
• 그렇기 때문에 이 다양한 형태로 구현된 것을 보고 배우면 오히려 혼란스러울 때가 많을 것이다.
• 그보다 더 상위 개념에 대해 이해를 하고, 이 개념을 다양한 프로그래밍 언어에서 처지에 맞게 구현해서 제공한다고 이해하는 것이 보다 좋다.
• 우리가 모나드를 이해하기 어려웠던 이유중 하나는 이 다양하게 구현된 형태를 모두 “모나드”라 부르는데서 오는 혼란이다.
• 지금까지는 조금더 쉬운 이해를 위해 Swift 언어를 가져와 설명했지만, 본격적으로 수학의 엄밀한 정의를 배워보도록 한다.
• 그 이후 각기다른 프로그래밍 언어에서 구현한 방법을 본다면, 다양한 형태가 모두 같은 것으로 보이게 될 것이다.

왜 알면 좋은가 2

• 또 하나 장점이 있다면, 함수형 프로그래밍 언어에서의 고급 기술은 “카테고리 이론”에 기반을 두기 때문이다.
• 결국 함수형 프로그래밍 자체에 관심이 있다면 언젠가는 고급 개념도 배워야 한다.
• Monad는 카테고리 이론에 기반을 둔 프로그래밍 개념중 두번째로 쉬운 개념이다 (?)
  • 첫번째는 Functor
• 이 다음으로 카테고리 이론에서 유래된 다른 개념들을 배우려면 Monad를 카테고리 이론과 연결지어 이해해야 한다.
  • 지금까지는 어찌보면 프로그래밍에 국한되어 Monad를 배운 것.

카테고리 이론 개념

• Functor
• Monad
• Adjunction
• Comonad
• Limit
• Applicative

얼마나 어려운가?

• 보통 다들 어렵다고 한다.
• 그런데 그 어렵다는 것이 “추상적”이어서 그렇게 들릴 가능성이 높다.
• 그나마 앞에서 예들을 보고 왔으니 그만큼 어렵게 들리지는 않을 것이다.

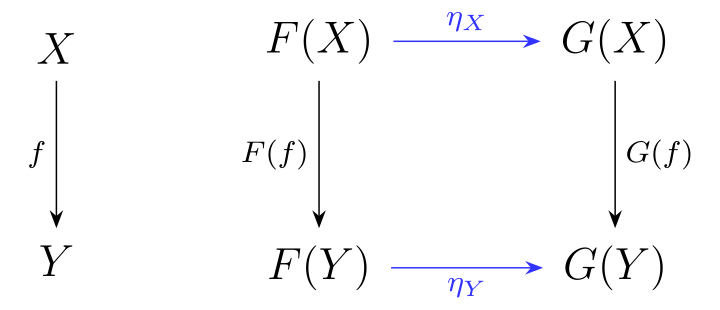
• 위키피디아에서 들고온 사진이다.
• 그림보면 어디서 많이 본 것 같지 않은가?
• 이정도의 개념을 이해한다면 도전해볼만 하다.

왜 어려운가?

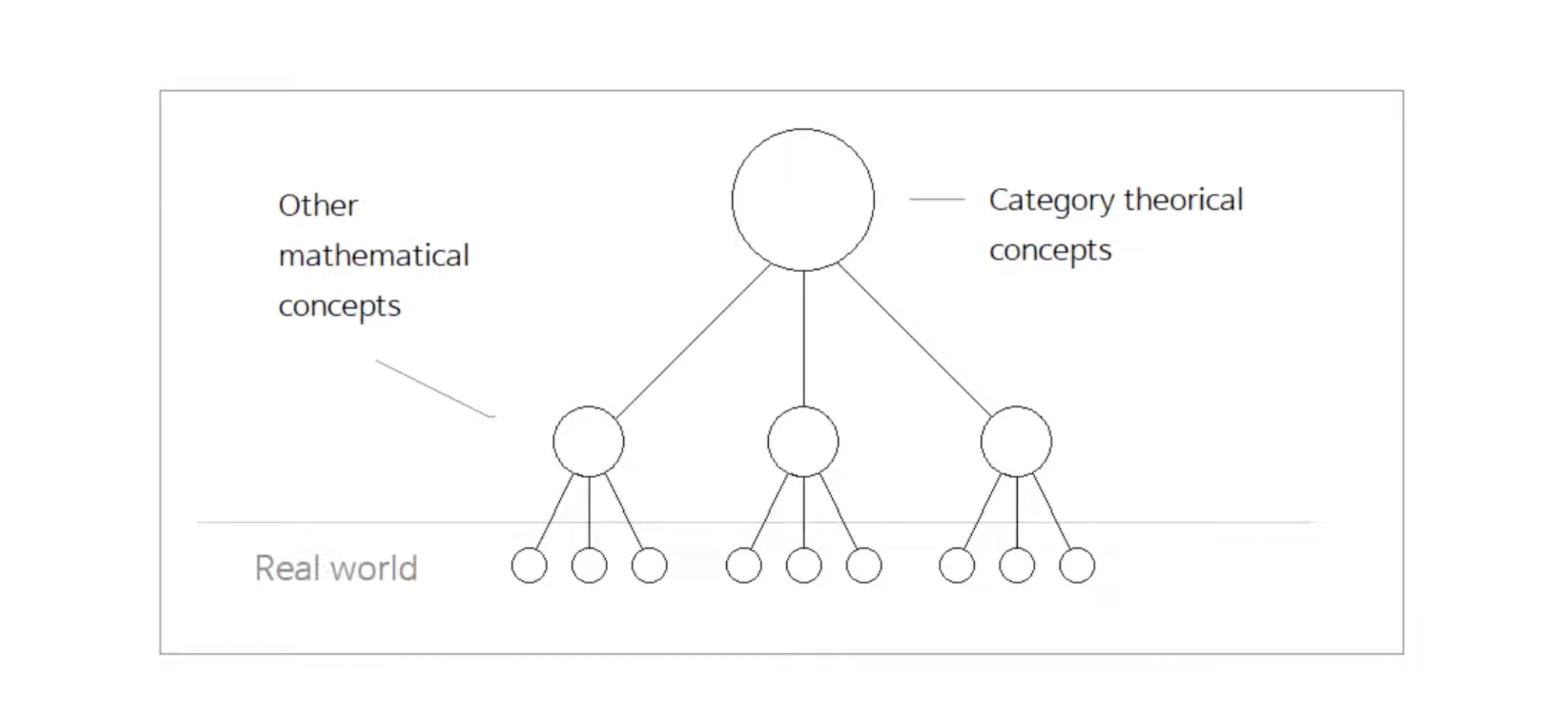
• 우리가 일반적으로 배우는 개념은 현실 세계와 개념이 밀접하게 연관되어 있다.
• 그렇기 때문에 예시를 들 수 있고, 그러면 이해가 빠르다.
• 하지만 카테고리 이론의 개념은 그 추상화된 것을 다시 모아 추상화한 것들이다.
• 정의를 기반으로한 사고가 아닌, 괜히 이상한 비유를 들었다간 더 혼란스러울 수 있다.

Reference

• 모나드의 모든 것
• FunctionalProgramming