Newton-Raphson Method

Tayler Series

테일러 급수는, 임의의 함수를 무한개의 다항식을 더하여 근사하는 방법이다.

$$\begin{gathered} f(x);=;f(a)+f^{\prime }(a)(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^{\prime \prime \prime }(a)}{2!}(x-a{)}^3\cdots \\ ; \\ ;=;\sum \_{n=0}^{\infty }\frac{f^n(a)}{n!}(x-a{)}^n \end{gathered}$$

보통 테일러 급수는 1차 함수로 근사할 때 많이 사용한다.

Newton-Rahpson method

뉴턴 랍슨 메서드의 핵심은, iterative 접근이다.

1변수 함수에서 Newton-Rahpson method

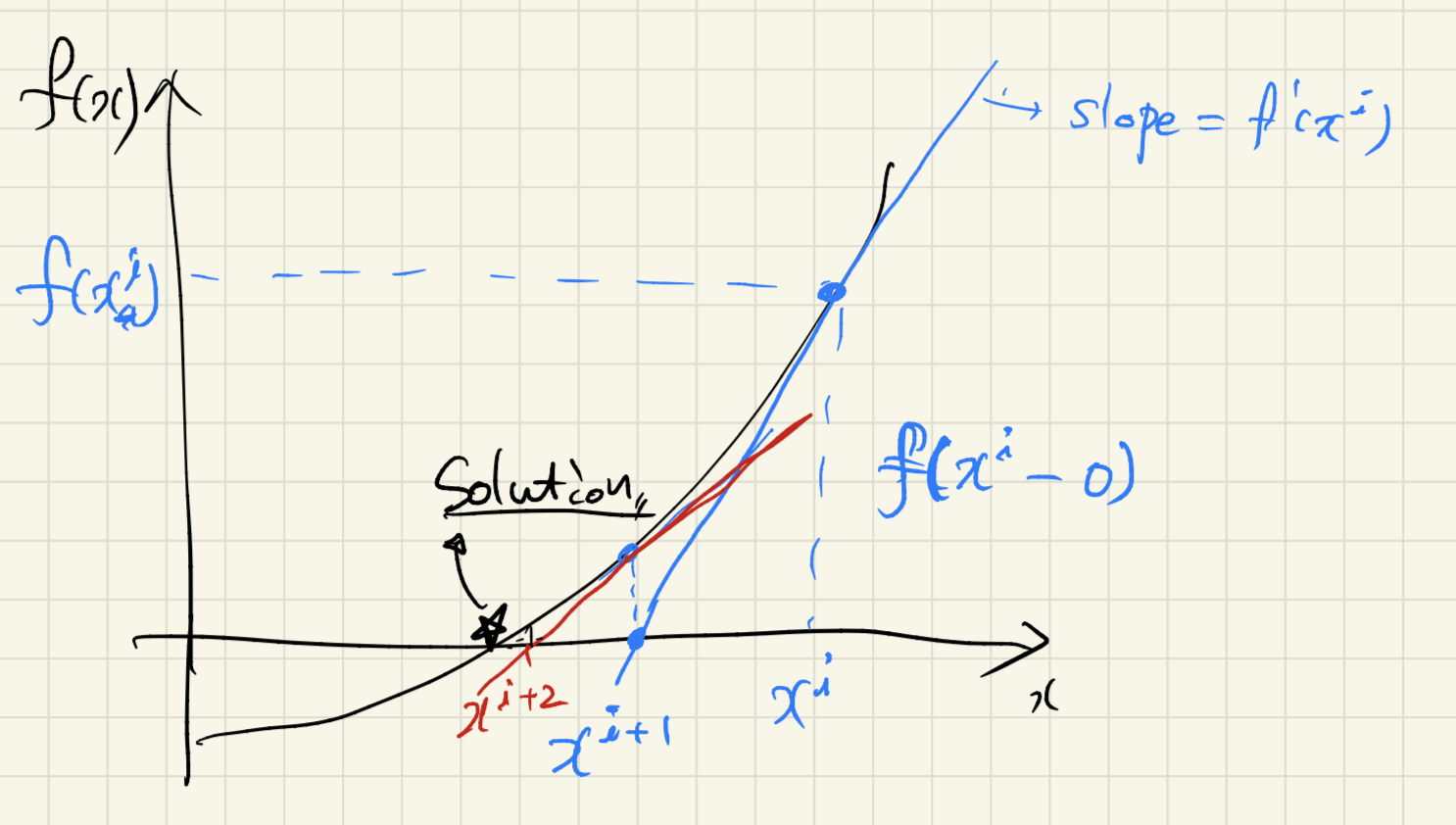
다음과 같은 함수가 있다고 하자. 우리가 하고 싶은 것은 이 함수의 근 을 찾는 것이다. 그러기 위해서 테일러 시리즈를 사용해보자. 이 함수 f는 1차까지만 근사하면 다음과 같다.

$$f(x);=;f(a)+f^{\prime }(a)(x-a)$$

이 때, 이 근사를 시작하는 점, a를 x_i로 주면,

$$f(x);=;f(x_i)+f^{\prime }(x_i)(x-x_i)$$

그렇다면 이 xi로 시작해서 이 함수를 근사했으므로, 근사한 식을 0으로 만드는 것이 답이다. **이 근사된 함수로 나온 solution을 x(i+1) 이라 하자.**

$$\begin{gathered} f(x\_i+1);=;f(x_i)+f^{\prime }(x_i)(x\_i+1-x_i) \\ ; \\ f(x\_i+1);=;f(x_i)+f^{\prime }(x_i)(\Delta x) \\ ; \\ f(x\_i+1);=;0을;만족하는;점이다. \end{gathered}$$

우리는 x_(i+1)을 찾고 싶으므로, 위의 가정들을 식에 다 집어넣으면,

$$\begin{gathered} f(x\_i+1);=;f(x_i)+f^{\prime }(x_i)(\Delta x_i);=;0 \\ ; \\ Delta{x}_i;=;-\frac{f(x_i)}{f^{\prime }(x_i)} \end{gathered}$$

따라서, 우리가 원하는 x_(i+1) 은 다음과 같다.

$$x\_i+1;=;x_i;+;\Delta x_i$$

나온 x_(i+1)을 다시 a로 넣고, 이 작업을 반복하게 되면, 해 근처에 갔을 때, 델타 x가 매우 작아진다. 이 때, 우리는 해를 찾았다고 return 해준다.

일반화된 Newton-Rahpson method

그렇다면, 식이 2개, 변수가 2개인 벡터 함수에서는 어떻게 근사할 수 있을까?

$$\begin{gathered} overset\to f(x,y);=; \\ beginbmatrix{f}_1(x,y) \\ {f}_2(x,y) \\ endbmatrix \end{gathered}$$

각각을 테일러 시리즈로 전개하자. 1차항 까지.

$$\begin{gathered} f_1(x\_i+1,y\_i+1);=;f_1(x_i,y_i)+\frac{\partial f_1}{\partial x}(x_i,y_i)(\Delta x_i)+;\frac{\partial f_1}{\partial y}(x_i,y_i)(\Delta y_i)=;0 \\ ; \\ {f}_2(x\_i+1,y\_i+1);=;f_2(x_i,y_i)+\frac{\partial f_2}{\partial x}(x_i,y_i)(\Delta x_i)+;\frac{\partial f_2}{\partial y}(x_i,y_i)(\Delta y_i)=;0 \end{gathered}$$

우변이 0인 이유는 위에서 설명한 것과 같은 의미 이다. 우리는 0이 되는 x, y를 찾고 싶은 것이기에 근사한 식에서 함수값이 0이 될 때, x*(i+1), y*(i+1) 이 필요하다. 편미분 후 x_i, y_i를 넣는 것을 생략해서 표현하면,

\\begin{bmatrix} \\partial f_1 \over \partial x & \partial f_1 \over \partial y\\ \\partial f_2 \over \partial x & \partial f_2 \over \partial y\\ \\end{bmatrix} \\begin{bmatrix} \\Delta x_i\\ \\Delta y_i\\ \\end{bmatrix} ;=; \\begin{bmatrix} -f_1(x_i, y_i)\\ -f_2(x_i, y_i)\\ \\end{bmatrix}

여기서,

J;=;\begin{bmatrix} \\partial f_1 \over \partial x & \partial f_1 \over \partial y\\ \\partial f_2 \over \partial x & \partial f_2 \over \partial y\\ \\end{bmatrix}

J를 자코비안 행렬 이라 한다.

\\Delta \overset{\rightarrow}{h} ;=; \\begin{bmatrix} \\Delta x_i\\ \\Delta y_i\\ \\end{bmatrix} ;=; \\begin{bmatrix} \\partial f_1 \over \partial x & \partial f_1 \over \partial y\\ \\partial f_2 \over \partial x & \partial f_2 \over \partial y\\ \\end{bmatrix}^{-1} \\begin{bmatrix} -f_1(x_i, y_i)\\ -f_2(x_i, y_i)\\ \\end{bmatrix} $$\begin{gathered} x\_i+1;=;x_i;+;\Delta x_i \\ ; \\ y\_i+1;=;y_i;+;\Delta y_i \end{gathered}$$

이므로 업데이트가 가능하다. 역시나 초기값 설정이 필요하다!

Position Analysis

이전 글에서 우리는 제약식들이 모인 벡터함수 C를 정의했다. 우리는 결국 벡터함수 C = 0 이되는 해, 즉 q 벡터를 찾는 것이 목적이다. 따라서 우리는 이 벡터 함수 C를 테일러 시리즈로 근사한 뒤 Newton-Rahpson method 를 사용해서 해를 구하자! 그러기 위해서는 벡터함수 C를 근사화 해야 한다. 테일러 시리즈를 적용하면,

$$\begin{gathered} overset\to C(\overrightarrow{q\_i+1};,t);=; \\ overset\to C(\overrightarrow{q\_i};,t);+;C\_q_i\Delta \overrightarrow{q_i};=;0 \end{gathered}$$ C\_{q_i};=;{\partial \overset{\rightarrow}{C} \over \partial \overset{\rightarrow}{q\_{i}}};=; \\begin{bmatrix} {\partial C_1\over \partial q_1} & \dots & {\partial C_1\over \partial q_n} \\\vdots\ & & \vdots\\ {\partial C_m\over \partial q_1} & \dots & {\partial C_m\over \partial q_n}\\ \\end{bmatrix}

C 행렬은 자코비안 행렬이다. 따라서,

\\Delta \overset{\rightarrow}{q_i};=;-\[ C\_{q_i}\]^{-1;}\overset{\rightarrow}{C}(\overset{\rightarrow}{q\_{i}};,t) $$overset\to q\_i+1;=;\overrightarrow{q_i};+;\Delta \overrightarrow{q_i}$$

로 q벡터를 구할 수 있다. 이를 반복하다가 특정 조건일 때, 우리는 반복을 멈추고 return 하면되는데,

$$\begin{gathered} \Vert \Delta \overrightarrow{q_i}|;\text{<};{ϵ}_1 \\ ; \\ OR \\ ; \\ \Vert \overrightarrow{C}(\overrightarrow{q\_i};,t)|;\text{<};{ϵ}_2 \end{gathered}$$

두 식의 의미는, 하나는 다가가는 step size이고, 두번째는 함수값의 size 차이이다.

해답을 찾아가는 과정에는 다음과 같이 두가지의 기준을 세울 수 있으므로, 두 기준에 대해서 iteration을 멈춘다.

Notice

우리는 t가 변수가 아닌 것에 주목해야 한다. 우리는 해를 수치적으로 구할 것이기 때문이다. t가 0일 때, q벡터의 초기값을 임의로 잡고, Newton 메서드, q 구함. t가 0.01 일 때, q벡터의 초기값을 임의로 잡고, newton 메서드 , q 구함. 따라서 t는 상수로 생각하고 우리는 문제를 푼다.

Velocity Analysis

같은 방법으로 제약식이 주어졌을 때, 우리가 궁금한 것은 q_dot 벡터이다.

$$overset\to C(\overrightarrow{q};,t);=;\overrightarrow{0}$$

이므로,

$$\frac{d\overrightarrow{C}(\overrightarrow{q},t)}{dt};=;\frac{d\overrightarrow{C}}{d\overrightarrow{q}}\cdot \stackrel{\cdot }{\overrightarrow{q}};+;\stackrel{\cdot }{\overrightarrow{C}};=;C\_q\cdot \stackrel{\cdot }{\overrightarrow{q}};+;\overrightarrow{C\_t};=;\overrightarrow{0}$$ $$\begin{gathered} overset\to C\_t;=; \\ beginbmatrix\frac{d{C}_1}{dt} \\ \frac{d{C}_2}{dt} \\ vdots \\ \frac{dC\_n_c}{dt} \\ endbmatrix \\ ; \\ {n}_c;=;제약식의;갯수 \end{gathered}$$

Ct 벡터는 t에 대해 미분한 벡터이므로, Driving constraint 식 이외 항은 0이다. 따라서 결론적으로,

C\_{q}\cdot \overset{\cdot}{\overset{\rightarrow}{q}} ;=;-\overset{\rightarrow}{C\_{t}}\\ ;\\ \\overset{\cdot}{\overset{\rightarrow}{q}};=; -\[ C\_{q}\]^{-1}\overset{\rightarrow}{C\_{t}}

이다.

Acceleration Analysis

제약식을 두번 미분해서, q_twodot 을 구하면 된다.

{d^2\overset{\rightarrow}{C}(\overset{\rightarrow}{q}, t) \over dt^2};=; {d\over dt}\[{d\overset{\rightarrow}{C} \over d\overset{\rightarrow}{q}}\cdot\overset{\cdot}{\overset{\rightarrow}{q}};+;\overset{\cdot}{\overset{\rightarrow}{C}}\] ;=; {d\over dt}\[ C\_{q}\cdot \overset{\cdot}{\overset{\rightarrow}{q}};+;\overset{\rightarrow}{C\_{t}}\] ;=;\overset{\rightarrow}{0}

결과적으로,

C\_{q}\cdot \overset{\cdot \cdot}{\overset{\rightarrow}{q}} ;=;\overset{\rightarrow}{Q\_{d}}\\ ;\\ \\overset{\cdot \cdot}{\overset{\rightarrow}{q}};=; \[ C\_{q}\]^{-1}\overset{\rightarrow}{Q\_{d}} \\ ;\\ \\overset{\rightarrow}{Q\_{d}};=;-( C\_{q} \overset{\cdot}{\overset{\rightarrow}{q}})*q \overset{\cdot}{\overset{\rightarrow}{q}};-;2 C*{qt} \overset{\cdot}{\overset{\rightarrow}{q}};-;\overset{\rightarrow}{C\_{tt}}