Monad와 Functor 사이에는 Monoidal Functor라는 중간 단계가 있다.

Monoidal Functor를 정의할 수 있는 언어

아무 언어에서나 정의될 수 있는 개념은 아니다. 다음의 조건이 선행되어야 한다.

Empty Type $()_0$ 을 제공해야 한다.
- Void
- ()
- C에서 빈 구조체 등
T, U 타입에 대한 Pair를 만들 수 있는 튜플 타입 $(T, U)_2$ 를 제공해야 한다.
튜플 타입과 빈 타입은 다음의 함수를 제공해야 한다.
- empty: $() \to ()_0$ - 빈 튜플을 만들어줌
- unite: $(T, U) \to (T, U)_2$ - 두 값을 튜플로 묶어줌
- e1: $(T, U)_2 \to T$
- e2: $(T, U)_2 \to U$

즉, 다음을 만족해야 한다.

unite(e1(u), e2(u)) = u

internal func empty() -> Void {
    ()
}
 
internal func unite<T, U>(_ t: T, _ u: U) -> (T, U) {
    (t, u)
}
 
internal func e1<T, U>(_ tu: (T, U)) -> T {
    tu.0
}
 
internal func e2<T, U>(_ tu: (T, U)) -> U {
    tu.1
}

unite 파생함수들

n개의 값을 n개가 하나의 타입안에 들어가도록 하는 unite_n을 알아보자. 즉, n개 인수를 하나의 인수로 바꿔준다.

unite_0 = empty
unite_1 = identity
unite_{n}(t1, ..., tn) = unite(unite_{n-1}(t1, ..., t{n-1}), t{n})

unite3(t1, t2, t3)
= unite1(unite2(t1, t2), t3)
= unite1(unite1(unite1(t1), unite1(t2)), unite1(t3))

하지만 이 함수는 완전 구현이 swift로 불가하다.
tuple이라는 자료구조의 인자 개수를 불특정한 상태로 선언할 수 없기 때문이다.
굳이 구현해본다면 이런 형태가 되겠다.

internal func unite0() -> Void {
    empty()
}
 
internal func unite1<T>(_ t: T) -> T {
    identity(t)
}
 
internal func unite2<T, U>(_ t: T, _ u: U) -> (T, U) {
    (t, u)
}
 
internal func unite3<T1, T2, T3>(_ t1: T1, _ t2: T2, _ t3: T3) -> ((T1, T2), T3) {
    unite2(unite2(t1, t2), t3)
}
 
internal func unite4<T1, T2, T3, T4>(_ t1: T1, _ t2: T2, _ t3: T3, _ t4: T4) -> (((T1, T2), T3), T4) {
    unite2(unite3(t1, t2, t3), t4)
}

unite_arg

그럼 이와 같은 형태의 함수도 만들 수 있을까?

unite_arg_3
: ((T1, T2, T3) -> U) -> (((T1, T2), T3) -> U)

internal func uniteArg3<T1, T2, T3, U>(_ f: @escaping ((T1, T2, T3) -> U)) -> (((T1, T2), T3)) -> U {
    { t12_3  in
        f(e1(e1(t12_3)), e2(e1(t12_3)), e2(t12_3))
    }
}

주어진 함수만으로 가능하다.

reassociate_r

reassociate_r
: ((T, U), V) -> (T, (U, V))

func reassociateR(tl: ((T, U), V))) -> (T, (U, V)) {
	unite(e1(e1(tl)), unite(e2(e1(tl)), e2(tl)))
}

reassociate_l

reassociate_l
: (T, (U, V)) -> ((T, U), V)

func reassociateL(tr: (T, (U, V))) -> ((T, U), V) {
	unite(unite(e1(tr), e2(e1(tr))), e2(e2(tr)))
}

Monoidal Functor 정의

다음을 만족하는 Functor M을 Monoidal Functor라 한다. 여기서 M은 Monoidal Functor를 의미한다.

pure: T -> M<T>
gather: Tuple(M<T>, M) -> M<Tuple(T, U)>

즉, Functor 중에서, lift가 있는 33. Generic중에 값을 33. Generic으로 확장할 수 있으면서

33. Generic의 튜플을 튜플의 33. Generic으로 만들어줄 수 있는 녀석을 말한다. Optional을 예로 코드를 첨부해본다.

internal func pure<T>(_ value: T) -> Optional<T> {
	Optional(value)
}
 
internal func gather<T, U>(_ tuple: (Optional<T>, Optional<U>)) -> Optional<(T, U)> {
    switch tuple {
    case (.some(let t), .some(let u)):
        return Optional((t, u))
    default:
        return nil
    }
}

Monoidal Functor의 조건

Conservation of associativity

Conservation of identity element

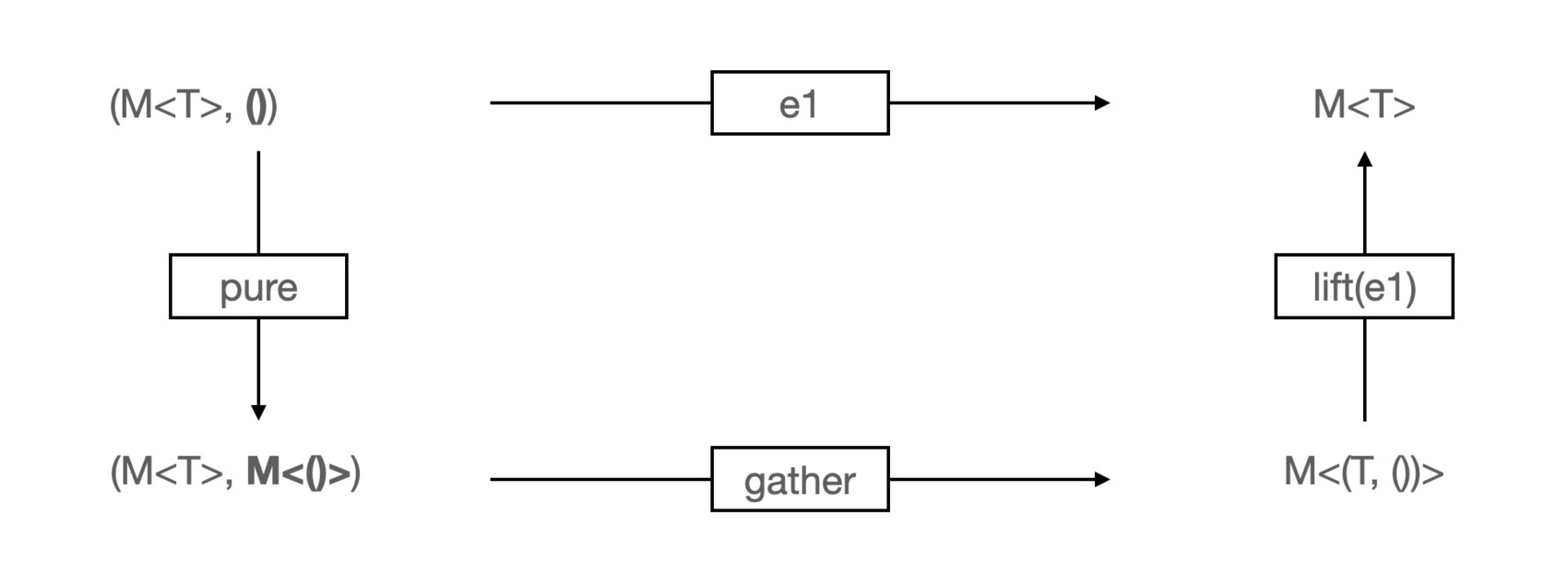
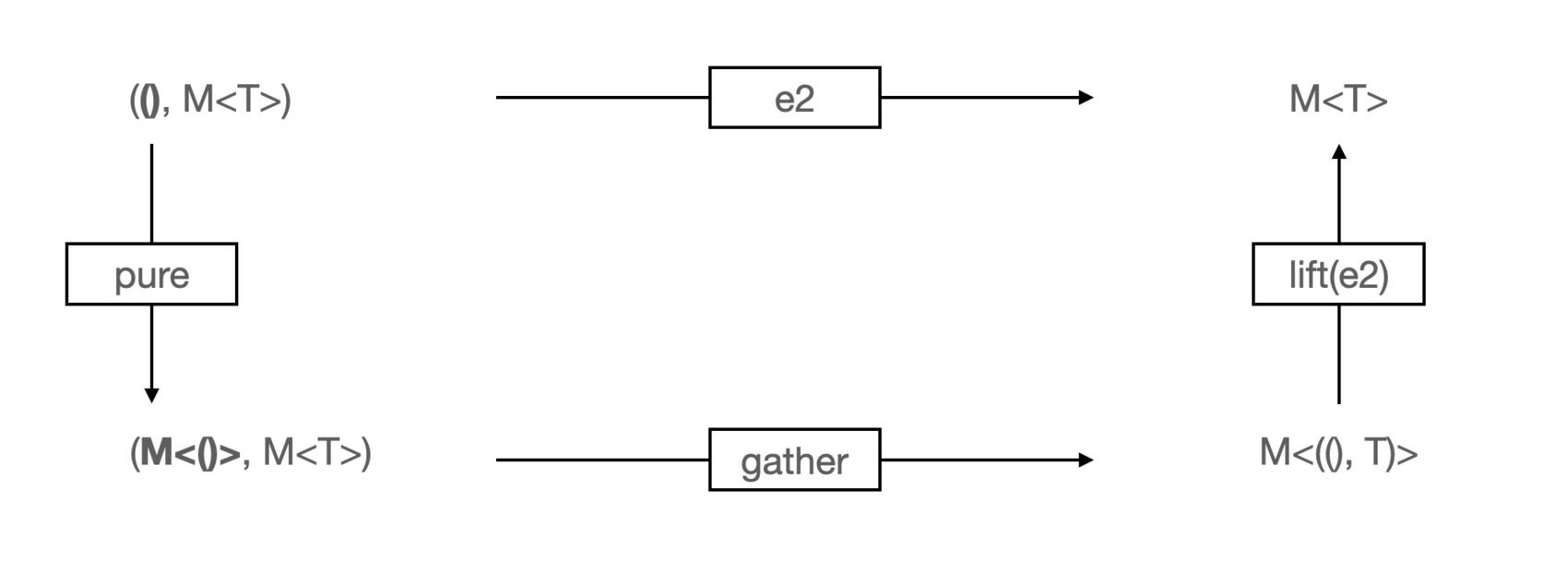
Monoidal Functor의 목적

다인수 함수의 자연스러운 lift를 위함

그런데 앞에서 functor만 가지고도 다인수 함수의 lift를 정의할 수 있지 않았나?
lift2d: ((T, U) -> V) -> ((F<T>, F) -> F<F<V>>)
하지만 인수 반환 타입에 Generic이 인수 개수만큼 들어가서 나온다.
lift2: ((T, U) -> V) -> ((M<T>, M) -> M<M<V>>)
우린 위와 같은 형태를 만들고 싶은 것이다.
혹은
lift0: (() -> U) -> (() -> M)
이런 형태도 정의해서 사용하고 싶다.
이런 조건을 요구하다보니 나온게 Monoidal Functor이다.
Monoidal Functor가 어떻게 다인수 함수의 lift를 원하는대로 만들 수 있는지 확인해보자.

m_unite_{n}

n개의 Monoidal functor를 튜플의 값으로 가지는 튜플을 하나의 Monoidal Functor로 만드는 함수

m_unite_{n}
(M<T1>, ..., M<T{n}>) -> M<(((T1, T2), T3), ..., T{n})>

m_unite_0 = pure(()) : (() -> M<T>)
m_unite_1(m1) = m1 : (M<T> -> M<T>)
m_unite_n(m1, ..., m{n}) = gather(unite(m_unite_{n-1}(m1, ..., m{n-1}), m{n}))
: (M<T1>, ..., M<T{n}>) -> M<(((T1, T2), T3), ..., T{n})>

위와 같이 재귀적으로 정의하면 된다.
이를 함수로 바꾸는 것은 어렵지 않다.

internal func mUnite0() -> Optional<Void> {
    pure(empty())
}
 
internal func mUnite1<T>(_ mt: Optional<T>) -> Optional<T> {
    identity(mt)
}
 
internal func mUnite2<T1, T2>(_ mt1: Optional<T1>,
                             _ mt2: Optional<T2>) -> Optional<(T1, T2)> {
    gather(unite(mt1, mt2))
}
 
internal func mUnite3<T1, T2, T3>(_ mt1: Optional<T1>,
                                  _ mt2: Optional<T2>,
                                  _ mt3: Optional<T3>) -> Optional<((T1, T2), T3)> {
    mUnite2(mUnite2(mt1, mt2), mt3)
}
 
internal func mUnite4<T1, T2, T3, T4>(_ mt1: Optional<T1>,
                                      _ mt2: Optional<T2>,
                                      _ mt3: Optional<T3>,
                                      _ mt4: Optional<T4>) -> Optional<(((T1, T2), T3), T4)> {
    mUnite2(mUnite3(mt1, mt2, mt3), mt4)
    // == mUnite2(mUnite2(mUnite2(mt1, mt2), mt3), mt4)
}

즉, 여기서 우리가 한 일은 연달아 나온 n개의 값을 nested한 하나의 튜플로 묶은 것이다.

lift_n

그럼 m_unite_n을 가지고 lift_n을 만들어보자.

lift_n
: ((T1, ..., T{n}) -> U) -> (M<T1>, ..., M<T{n}) -> M<U>

internal func lift3<T1, T2, T3, U>(_ f: @escaping ((T1, T2, T3) -> U)) -> (T1?, T2?, T3?) -> U? {
    { mt1, mt2, mt3 in
        lift(uniteArg3(f))(mUnite3(mt1, mt2, mt3))
    }
}

재밌는 건 lift_n을 가지고 m_unite_n도 만들 수 있다는 것이다.

internal func lift3<T1, T2, T3, U>(_ f: @escaping ((T1, T2, T3) -> U)) -> (T1?, T2?, T3?) -> U? {
    { mt1, mt2, mt3 in
        lift(uniteArg3(f))(mUnite3(mt1, mt2, mt3))
    }
}
 
internal func unite3<T1, T2, T3>(_ t1: T1, 
								 _ t2: T2, 
								 _ t3: T3) -> ((T1, T2), T3) {
    unite(unite(t1, t2), t3)
}
 
internal func mUnite3<T1, T2, T3>(_ mt1: T1?,
                                  _ mt2: T2?,
                                  _ mt3: T3?) -> ((T1, T2), T3)? {
    mUnite2(mUnite2(mt1, mt2), mt3)
}
 
internal func mUnite3<T1, T2, T3>(_ mt1: T1?,
                                  _ mt2: T2?,
                                  _ mt3: T3?) -> ((T1, T2), T3)? {
    lift3(unite3)(mt1, mt2, mt3)
}

mUnite3 = lift3(unite3)

이 얘기는 mUnite_n과 lift_n이 서로를 통해 정의할 수 있는 동치 관계에 있음을 의미한다.

pure와 gather

pure와 gather 역시 lift를 사용하여 정의 가능하다.

internal func pure<T>(_ value: T) -> Optional<T> {
    Optional(value)
}
 
internal func pureFromLift<T>(_ value: T) -> Optional<T> {
    lift0 { () -> T in
        value
    }()
}

internal func gather<T, U>(_ tuple: (Optional<T>, Optional<U>)) -> Optional<(T, U)> {
    switch tuple {
    case (.some(let t), .some(let u)):
        return Optional((t, u))
    default:
        return nil
    }
}
 
internal func gatherFromLift<T, U>(_ tuple: (Optional<T>, Optional<U>)) -> Optional<(T, U)> {
    mUnite2(e1(tuple), e2(tuple))
}

정리해보자.

아래 4개의 함수가 동작하는 언어여야 Monoidal Functor는 정의된다.

enum Summary {
 
}
 
extension Summary {
 
    internal func empty() -> Void {
        ()
    }
 
    internal func unite<T, U>(_ t: T, _ u: U) -> (T, U) {
        (t, u)
    }
 
    internal func e1<T, U>(_ tu: (T, U)) -> T {
        tu.0
    }
 
    internal func e2<T, U>(_ tu: (T, U)) -> U {
        tu.1
    }
 
}

Monoidal Functor가 되기 위한 조건, 아래의 두 함수만 정의되면 된다.

extension Summary {
 
 
 
    internal func pure<T>(_ t: T) -> T? {
        Optional(t)
    }
 
    internal func gather<T, U>(_ tuple: (T?, U?)) -> (T, U)? {
        switch tuple {
        case (.some(let t), .some(let u)):
            return Optional((t, u))
        default:
            return nil
        }
    }
 
}

이상황에서 우리가 하고 싶은게 뭘까?
우리가 하고 싶은 건 다인수 함수의 lift를 잘 정의하는 것이다.
((T1, T2, T3) → U)) → (T1?, T2?, T3?) → U? 이런 형태.
먼저 unite_n을 정의하자. n개에 대해서는 안되니 3개까지만 해보자.

extension Summary {
 
    internal func unite0() -> Void {
        empty()
    }
 
    internal func unite1<T>(_ t: T) -> T {
        identity(t)
    }
 
    internal func unite2<T1, T2>(_ t1: T1, _ t2: T2) -> (T1, T2) {
        (t1, t2)
    }
 
    internal func unite3<T1, T2, T3>(_ t1: T1, _ t2: T2, _ t3: T3) -> ((T1, T2), T3) {
        unite(unite(t1, t2), t3)
    }
 
}

다음으로 m_unite_n을 정의하자.

extension Summary {
 
    internal func mUnite0() -> Void? {
        pure(empty())
    }
 
    internal func mUnite1<T>(_ mt: T?) -> T? {
        identity(mt)
    }
 
    internal func mUnite2<T1, T2>(_ mt1: T1?,
                                  _ mt2: T2?) -> (T1, T2)? {
        gather(unite(mt1, mt2))
    }
 
    internal func mUnite3<T1, T2, T3>(_ mt1: T1?,
                                      _ mt2: T2?,
                                      _ mt3: T3?) -> ((T1, T2), T3)? {
        mUnite2(mUnite2(mt1, mt2), mt3)
    }
 
}

마지막 하나의 함수만 더 정의하자. uniteArg3.

extension Summary {
 
    internal func uniteArg3<T1, T2, T3, U>(_ f: @escaping ((T1, T2, T3) -> U)) -> (((T1, T2), T3)) -> U {
        { t12_3  in
            f(e1(e1(t12_3)), e2(e1(t12_3)), e2(t12_3))
        }
    }
 
}

이제 lift 함수를 만들어보자.

extension Summary {
 
    internal func lift2<T1, T2, U>(_ f: @escaping ((T1, T2) -> U)) -> (T1?, T2?) -> U? {
        { mt1, mt2 in
            lift(f)(mUnite2(mt1, mt2))
        }
    }
 
    internal func lift3<T1, T2, T3, U>(_ f: @escaping ((T1, T2, T3) -> U)) -> (T1?, T2?, T3?) -> U? {
        { mt1, mt2, mt3 in
            lift(uniteArg3(f))(mUnite3(mt1, mt2, mt3))
        }
    }
 
}

그런데 lift3로 mUnite3을 표현할 수 있다.

extension Summary {
 
    internal func mUnite2FromLift<T1, T2>(_ mt1: T1?,
                                          _ mt2: T2?) -> (T1, T2)? {
        lift2(unite2)(mt1, mt2)
    }
 
    internal func mUnite3FromLift<T1, T2, T3>(_ mt1: T1?,
                                              _ mt2: T2?,
                                              _ mt3: T3?) -> ((T1, T2), T3)? {
        lift3(unite3)(mt1, mt2, mt3)
    }
 
}

뭔가 이상하다. lift를 찾아온 여정인데, 그결과로 자신을 정의할 수 있다니.
즉 동치인 구조를 발견한 것이다.

동치 구조

이 부분에서 막혀서 여러가지 시도를 해보았다.
만지작 거려보면, 함수들이 서로 순환하면서 내가 정의되기 위해서는 다른 함수가 요구되는 상황이 펼쳐진다.

enum Veritication {
 
}
 
extension Veritication {
 
    // 필요 함수
 
    internal func lift0<T>(_ transform: @escaping () -> T) -> (() -> T?) {
        { () -> T? in
            transform()
        }
    }
 
    internal func lift<T, U>(_ transform: @escaping (T) -> U) -> (Optional<T>) -> Optional<U> {
        return { (input: Optional<T>) -> Optional<U> in
            switch input {
            case .none:
                return .none
            case .some(let wrapped):
                return .some(transform(wrapped))
            }
        }
    }
 
    internal func lift2<T1, T2, U>(_ f: @escaping ((T1, T2) -> U)) -> (T1?, T2?) -> U? {
        { mt1, mt2 in
            lift(f)(mUnite2(mt1, mt2))
        }
    }
 
    internal func unite2<T1, T2>(_ t1: T1, _ t2: T2) -> (T1, T2) {
        (t1, t2)
    }
 
    // 증명 시작
 
    internal func pure<T>(_ t: T) -> T? {
        Optional(t)
    }
 
    internal func pureFromLift<T>(_ value: T) -> Optional<T> {
        lift0 { () -> T in
            value
        }()
    }
 
    internal func gather<T, U>(_ tuple: (T?, U?)) -> (T, U)? {
        switch tuple {
        case (.some(let t), .some(let u)):
            return Optional((t, u))
        default:
            return nil
        }
    }
 
    internal func gatherFromLift<T, U>(_ tuple: (Optional<T>, Optional<U>)) -> Optional<(T, U)> {
        //        mUnite2(e1(tuple), e2(tuple))
        mUnite2FromLift(e1(tuple), e2(tuple))
    }
 
    internal func mUnite2<T1, T2>(_ mt1: T1?,
                                  _ mt2: T2?) -> (T1, T2)? {
        gather(unite(mt1, mt2))
    }
 
    internal func mUnite2FromLift<T1, T2>(_ mt1: T1?,
                                          _ mt2: T2?) -> (T1, T2)? {
        lift2(unite2)(mt1, mt2)
    }
 
}

결론

Monoidal Functor는 Functor가 lift_n을 갖기 위한 필요충분조건이다.

Monoidal Functor는 pure, gather만 정의했다.
그리고 그 상황에서 lift_n이 우리가 원하는 꼴로 정의되는지 확인해봤다.
그랬더니 lift_n이 잘 정의되었다!

혹은.

lift_n이 정의되는 조건을 찾았다.
그럴 경우 pure, gather함수는 무조건 만족한다.
즉, Monoidal Functor는 다인수 함수의 lift를 원하는 꼴로 만드는 녀석이다.

양쪽 모두 같은 결론에 도달하고 있다. 이 결과를 통해 Monoidal Functor가 Functor와 Monad 사이 범주에 해당하는 녀석임을 확인할 수 있다.

왜 많이 사용되지 않는가?

함수형 언어에서 다인수 함수의 인자를 튜플을 사용하지 않기 때문.
- 반대로 말하면 n-tuple을 잘 지원하는 언어에서는 이 개념이 주류가 되었을 것.
튜플말고 함수형 언어 환경에서 더 잘 활용될 수 있을 만한 개념을 넣을 수 있는데,
apply: M<T->U> -> (M<T>->M)이다.
해당 함수를 사용하는 방식이 곧 10. Applicative Functor이다.

🥚

Explorer

Recent Notes

2024-10

Hessian Matrix

Jacobian Matrix

Monoidal Functor