Sorting

정렬에 대해 깊게 공부해보자.

• 제자리 정렬
  • 정렬을 하는데 필요한 추가 저장공간이 상수인 경우
• 안정성
  • 같은 키 값([3, 3])을 가지는 데이터간의 정렬전 순서가 정렬 후에도 유지되는 경우
  • 즉 3_1, 3_2가 있었는데 정렬 끝나니까 3_2, 3_1이렇게 되어있었다면 불안정한 것

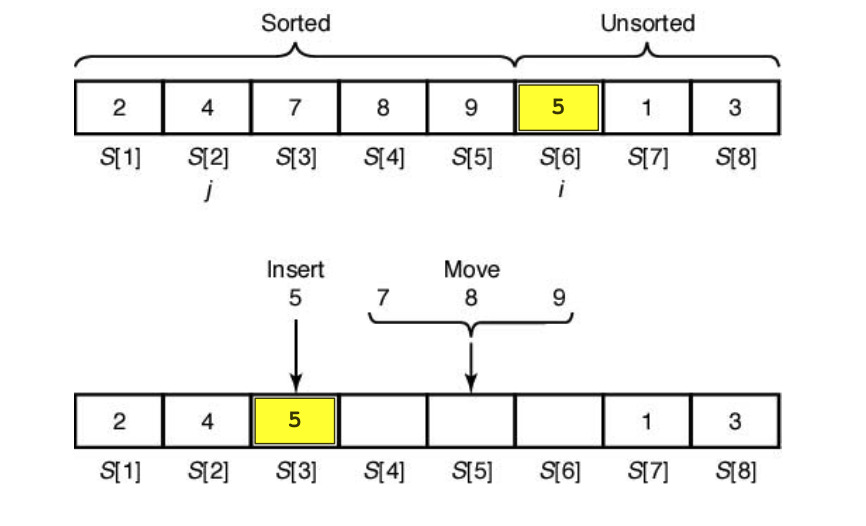삽입 정렬

삽입 정렬

• 항목을 끼워 넣는다고 생각해!!!
• 어디에? : 앞에
• 앞에는 이미 정렬이 되어 있는거야. 내 원소를 삽입해서 정렬된 상태로 만들고 싶은 거지
• 그럼 앞에 정렬되어 있으면 뒤가 안되어 있겠네
• 그러니까 2번부터 시작해서 n까지 갈 때, (i)
• i-1번째 원소부터 나랑 비교하면서 내가 더 작으면 자리를 바꾸는거야

def insertsort(a):
  for i in range(1, len(a)):
    j = i-1
    x = a[i]
    while j >= 0 and a[j] > x:
      a[j+1] = a[j]
      j -= 1
    a[j+1] = x
  return a

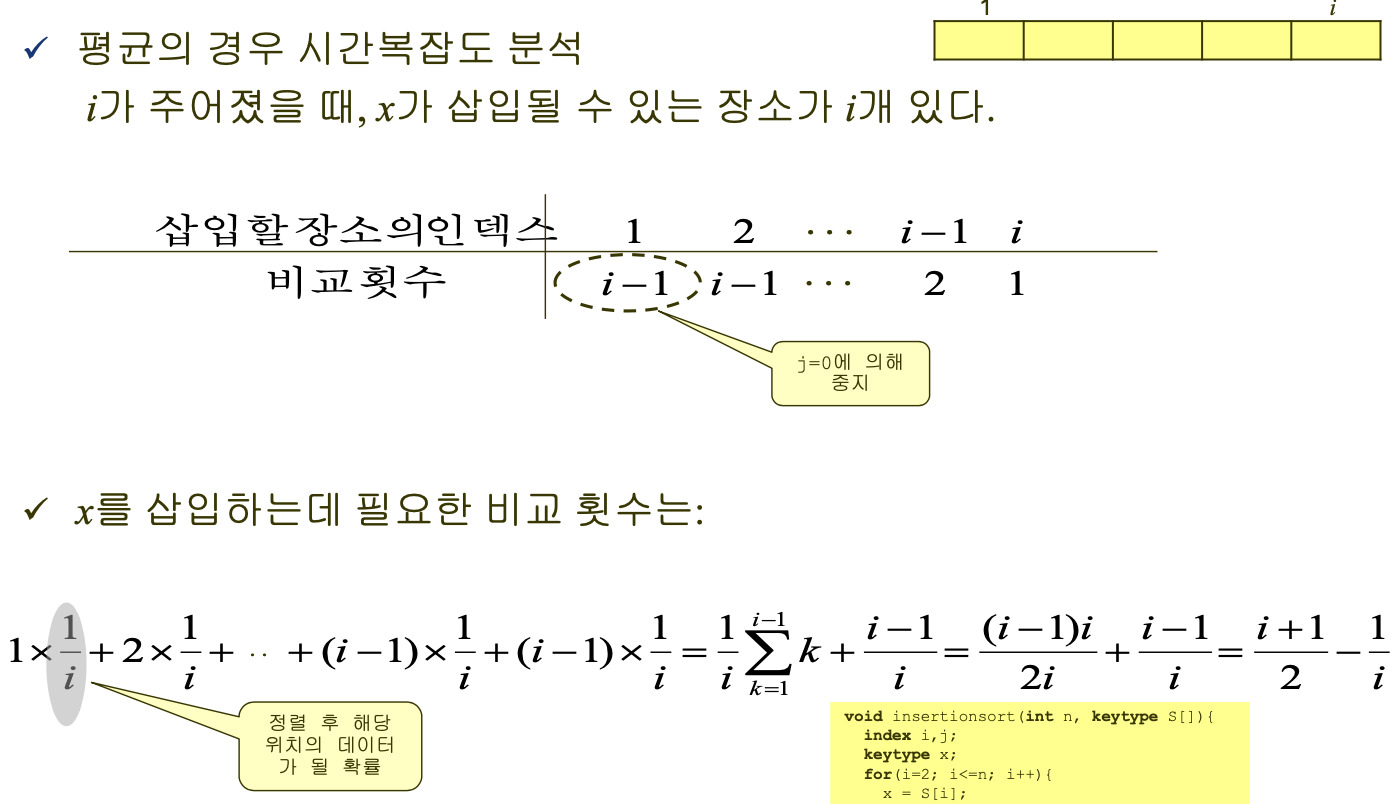
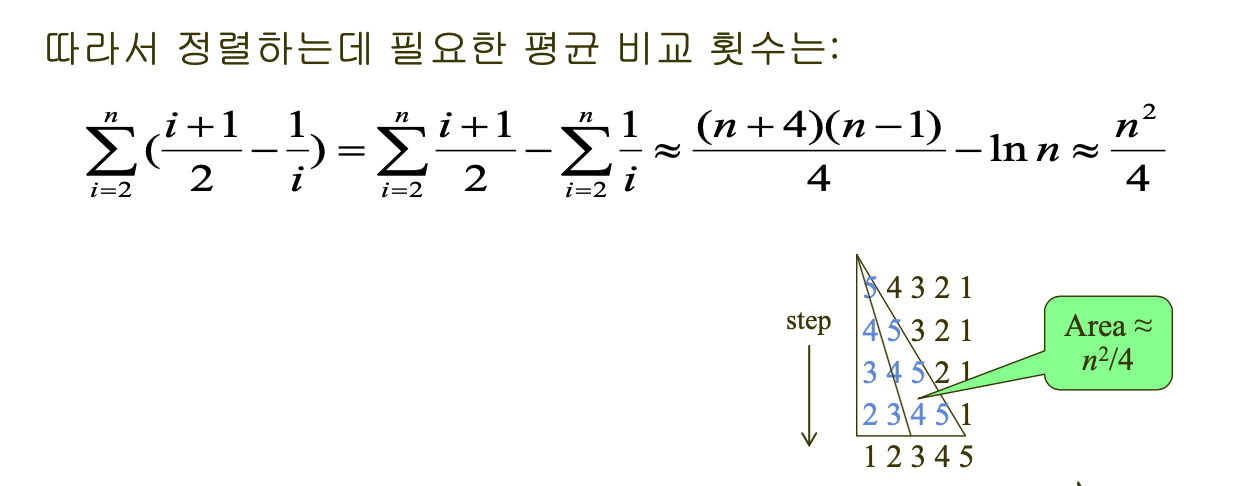
평균 계산은, 시작 위치가 2부터 이므로, 그 시작위치에 따른 계산의 횟수를 구하고 그 비교 횟수를 확률 변수 X로 둔다. 그리고 그 비교 횟수가 등장하기 위한 확률은 i에 따라 결정된다. 즉, i가 2부터 n까지 가는데, 각각의 i가 등장할 확률은 1/(i-1)이다. 그런데 1까지 인덱스가 갈수는 있으므로 결국 해당 index가 등장할 확률은 고르게 1/i이다.

나머지는 기대값을 계산해주면 된다. 그런데 기하학적으로 보아도 당연한 결과가 나온다.

얘는 뒤에 있는 값을 앞으로 넣으면서 계속해서 앞의 값을 뒤로 교환한다. 그렇기 때문에 [5, 4, 3, 2, 1]의 경우 1+2+3+4번, 얘도 P(n^2)이다. 평균은 그것의 반

선택 정렬

선택 정렬

• 뒤에서 부터 제일 작을 놈을 선택해서 넣어버린다.
• 불안정 정렬
  • 실제로 해보면 자리가 변경된다.
• 제자리 정렬

def selectionsort(a):
  for i in range(0, len(a)-1):
    minIdx = i
    for j in range(i+1, len(a)):
      if a[j] < a[minIdx]:
        minIdx = j
    temp = a[i]
    a[i] = a[minIdx]
    a[minIdx] = temp
  return a

선택 정렬은 기본적으로 뒤에 있는 원소를 살펴보고, 시작하는 위치랑 비교해서 작을 경우 값을 변경해주는 방식이다. 이후 나올 교환정렬보다 교환 횟수가 적다는 장점이 있다. 그리고 공간복잡도는 변하지 않고, 그냥 n이고, 제자리 정렬이고, 최소값을 앞에 선택한 원소와 변경하기 때문에 불안정정렬이다. [4, 4, 1, 5] 해보면 바로 안다.

선택정렬은 지정하는 것이 다 찾고 한번 한다. 그렇기 때문에 O(n), 정확히는 3(n-1)이다.

교환 정렬

• i번째와 j번째를 아주그냥 계속 교환해버리는 거야
• [4a, 4b, 1, 5] → 아주 그냥 계속 바뀌어 - 불안정 정렬
• 제자리 정렬

def exchangesort(a):
  for i in range(len(a)-1):
    for j in range(i+1, len(a)):
      if a[j] < a[i]:
        temp = a[i]
        a[i] = a[j]
        a[j] = temp
  return a

교환 정렬은 실제로 교환을 많이 한다. 그렇기 때문에 단점이 많다. 이전의 알고리즘보다 교환의 횟수가 증가하는 경향이 있다. [4, 4, 1, 5]를 해보면 계속 교환이 되기 때문에 불안정하다는 것을 알 수 있다. 그리고 제자리 정렬이다.

지정하는데 있어서 n^2번 돌면서 다 지정하기 때문에 지정도 n^2, 시간 복잡도도 n^2이다.

거품 정렬

거품 정렬

• 얘는 뒤에서부터 시작해서 작은 값이 거품처럼 올라온다고 거품 정렬이다.

def bubblesort(a):
  for i in range(len(a)-1):
    for j in range(len(a)-2, i-1, -1):
      if a[j+1] < a[j]:
        temp = a[j+1]
        a[j+1] = a[j]
        a[j] = temp
  return a

• 교환정렬과 방법만 다르지 시간 복잡도, 공간복잡도, 지정복잡도는 다 같다.

정리

기본 정렬 정리

• 삽입 정렬은 애초에 정렬되어 있는 걸 가정하고 하기 때문에 정렬이 어느정도 되어 있으면 더 빠르다.
• 삽입 정렬은 교환정렬보다는 빠른 경향이 있다고 말해도 된다. 애초에 교환 정렬이 별로다.
• 선택 정렬과 교환 정렬? 선택 정렬이 낫다. 지정을 덜하니까
• 그럼 이미 정렬이 되어 있다면?
  • 교환 정렬은 지정하지 않는다.
  • 선택 정렬은 교환이 이루어진다 (? 아닌거같지? 근데 처음 시작지점이 나부터 시작하니까 마지막에 교환을 무조건 한번하잖아.)
• 선택 정렬이 삽입 정렬보다 빠른가?
  • 일단 삽입 정렬이 동작하는 방식을 보면 앞에 있는 것을 계속 민다.
  • 민다는 것은 지정이 많이 된다는 것
  • n이 커질 경우 지정역시 무시할 수 없기 때문에 선택이 보다 낫다고 할 수 있다.

한번 비교하는데 최대한 하나의 역을 제거하는 알고리즘의 하한선

?? 이게 도대체 무슨말이야. 일단 아래를 보며 이해하자.

• n개의 키, 양의 정수 1~n을 가정하자.
• n개의 양수는 n!개의 순열이 존재한다. (n개를 나열한다고 했을 때)
• $k_i$를 i번째 자리에 위치한 정수라고 하면 [k1, k2, ..., kn으로 나타낼 수 있다.
• i < j와 ki > kj를 만족하는 쌍 (ki, kj)를 순열에 존재하는 역(inversion)이라 한다.
• [3, 2, 4, 1, 6, 5]에는 5개의 역이 존재
  • {(3, 2), (3, 1), (2, 1), (4, 1), (6, 5)}

즉, 배열이 있고, 거기서 역이라는 쌍을 만들 건데, 거기서 하나의 역을 제거할 때 걸리는 시간복잡도의 하한을 구해보자는 의미. 즉 가장 효율적으로 했을 때 시간복잡도가 얼마일까?

• 최악의 경우
  • 최악의 경우는 내림차순으로 정렬되어 있을 때이다.
  • 그러면 그 원소에서 2개를 뽑기만 하면(조합) 모두 역이다. (역인지는 알겠지만 일단 모른다고 해보자.)
  • 모르면, 발생하는 모든 쌍에 대해 역인지 체크하고 지워야 한다. 그럼 일단 뽑는게 $\frac{n(n-1)}{2}$가 될텐데(nC2), 한번 두 원소를 비교하면 되니까 총 비교횟수는 $\frac{n(n-1)}{2}$
• 평균적으로
  • 자 원래 배열을 뒤집어 보자. 그걸 A’이라 하자.
  • 그러면 A에서 쌍을 뽑을 수 있고 A’에서 쌍을 뽑을 수 있다.
  • 그러면 그 두개에서 발생하는 쌍은 총 n(n-1)개이다.
  • 근데 그중에서 역을 만족하는 것은 정확하게 반이다.
  • 결과적으로 A하나의 배열에서 나올 수 있는 역의 개수는 평균적으로 $\frac{n(n-1)}{4}$이다.

자 이얘기를 왜 했느냐.

• 교환
• 삽입
• 선택
• 버블

정렬의 경우 결국 이러한 역에 관련된 것을 찾고, 이를 비교하여 바꾸는 연산을 하는 것이다. 그렇기 때문에 위의 4개의 정렬 알고리즘은 이러한 경향을 그대로 따르게 되는데, 해당 문제의 알고리즘의 하한이 최악의 경우 $\frac{n(n-1)}{2}$이고, 평균적으로 $\frac{n(n-1)}{4}$ 인 것을 밝혔으므로, 위의 4 알고리즘의 한계를 알아낸 것.

Merge Sort

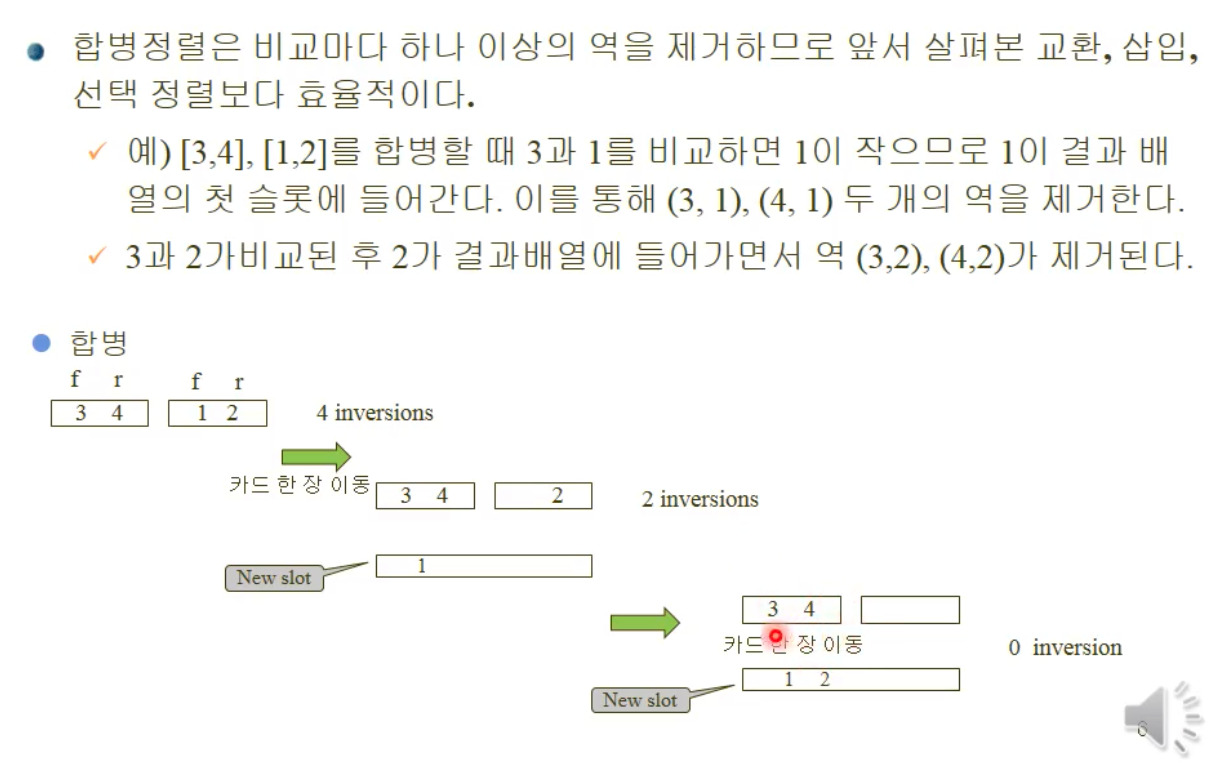합병 정렬 알고리즘 재검토

그러면 합병 정렬은?

• 합병 정렬 같은 경우 나뉜 두개의 공간에서 포인터를 이용하여 이를 합치는 작업을 하게 된다.
• 그런데, 그 각각의 공간은 정렬이 되어 있기 때문에, 새로운 공간에 하나의 원소가 들어갔지만 실질적으로는 2개의 역이 사라진 효과를 가지게 된다.

Quicksort

pivot 놓고 양쪽으로 나누어서 재귀적으로 진행하는 알고리즘. 다 알재?

Heap Sort

Binary Tree의 종류

이진 트리의 종류

• 완전 이진 트리
  • 트리 내부에 있는 모든 마디에 두 개씩 자식 마디가 있는 이진 트리
  • 완전하기 때문에 리프의 depth가 모두 동일
• 실질적인 완전 이진 트리
  • 사실 이러한 것이 되기 어려움
  • 그래서 쭉 넣는데, 마지막 depth를 다 못채워서 왼쪽 부터 채운 것
  • 즉, d-1까지는 완전 이진 트리, d에서는 왼족부터 채워진 이진 트리
• Full 이진 트리
  • 모든 노드가 0또는 2개의 자식 노드를 갖는다.

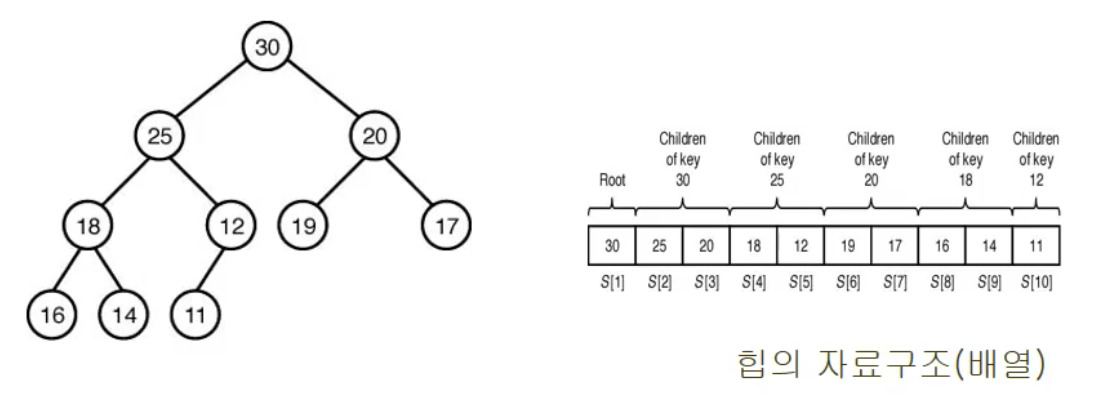Heap

Heap

• 어떤 마디에 저장된 값은 그 마디의 자식 마디에 저장된 값보다 크거나 같다. (max heap)
• 얘는 실질적인 완전 이진트리이다.
• 특징
  • 최대값의 확인 : O(1)
  • 최대값 제거 및 재구성 : O(logn)
    • depth가 logn이기 때문에 없애고 재구성
    • 결국 재구성할 때 logn만큼의 depth만 타고 내려가면 된다.
  • 데이터의 추가, 삭제 변경 : O(logn)
    • 추가도 재구성
    • 삭제도 재구성
    • 변경도 재구성이기 때문
  • 우선 순위 큐를 구현하는데 적합

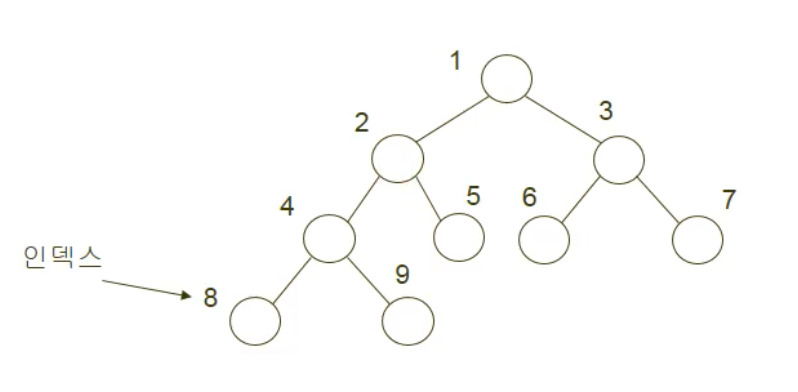Heap 구조

• 구조 해석
  • index i 노드
    • Left = 2*i
    • Right = 2*i + 1
    • 부모 접근 방법 : int(left or right / 2)

Sift down

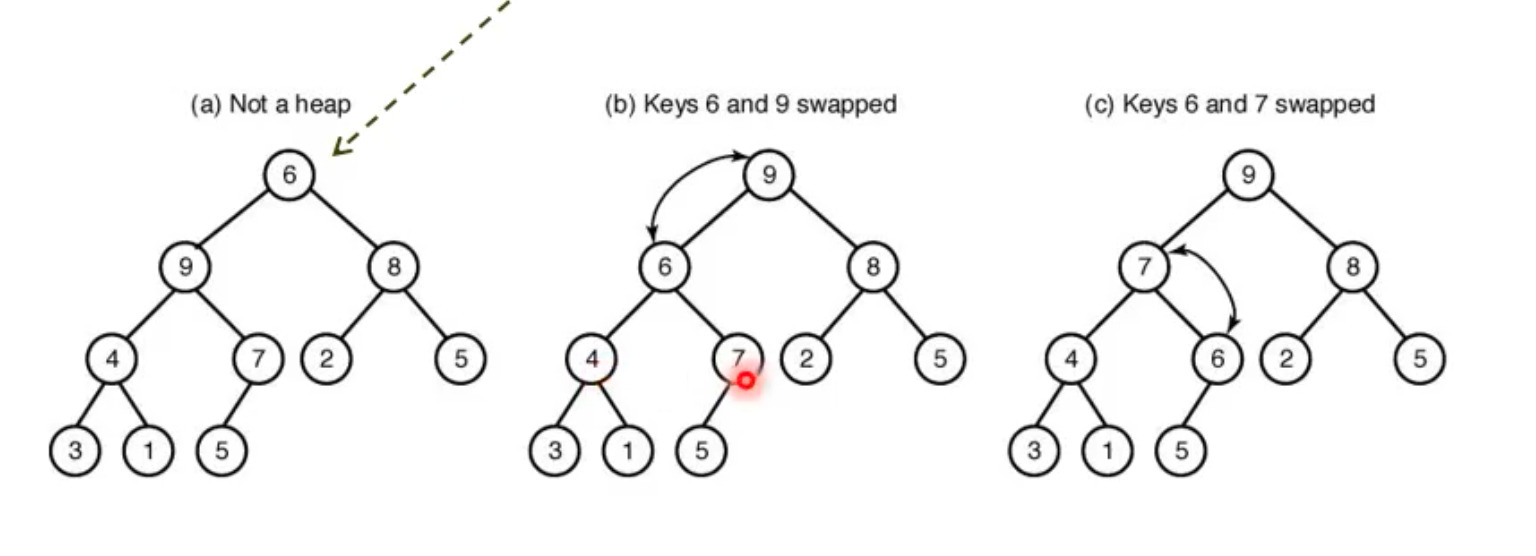Sift down

루트에 있는 키가 Heap 성질을 만족하지 않을 때, 이를 만족시키도록 하는 방법

Heap sort 설명

1. n개의 키를 사용하여 heap을 구성한다.
   • 데이터를 순차적으로 입력하면서 Heap을 구성 (siftUp) - O(nlogn)
   • 이미 배열에 데이터를 넣어두고 Heap을 구성(Siftdown) - O(n)
2. 루트를 제거한다. - O(1)
3. heap을 재구성한다. - O(logn)
4. 2를 반복한다.

Sift up

data = [2, 4, 5, 3, 1, 9, 6, 7, 10, 8]

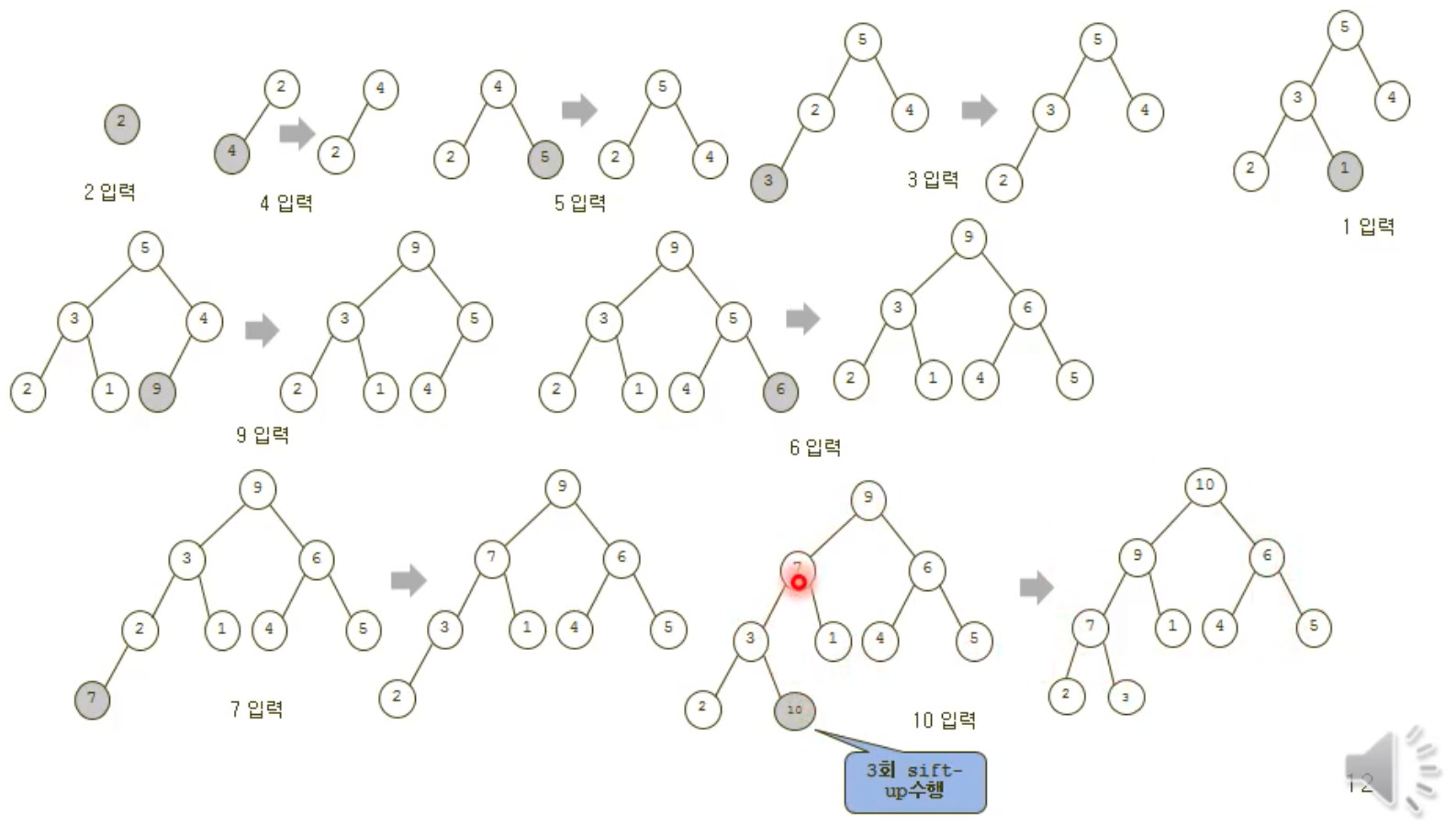
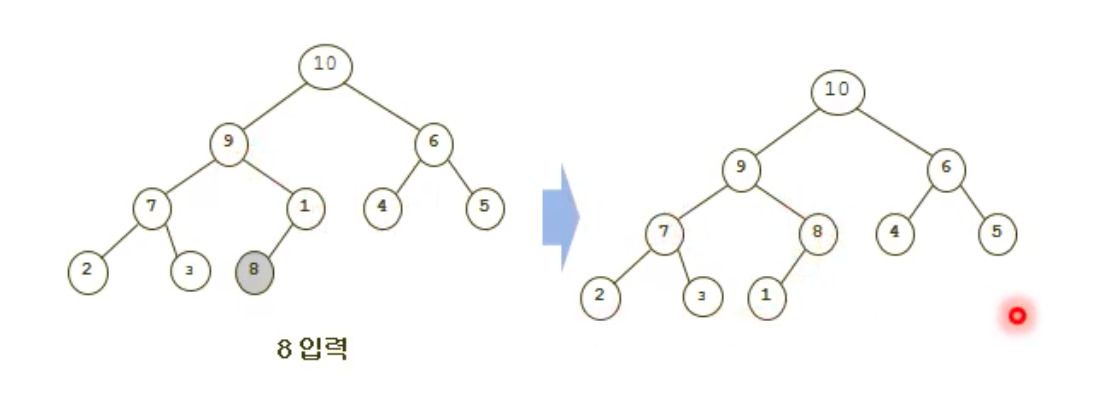
• 핵심은 추가가되면 가장 맨 끝의 index에 추가하고, 거기서부터 부모노드를 찾으면서 자기 자리를 찾는 방법
• 시간 복잡도
  • 단위 연산 : 키의 비교
  • 입력 크기 : n(총 키의 개수), = 2^k라 가정
  • depth = log(n)
  • 새롭게 키가 추가되면 d+1의 depth에 위치함 (n=2^k 가정)
  • 그러면 d개의 조상을 가짐
  • 자 그러면 처음 시작부터 몇개의 비교를 하는지 표로 살펴보자.

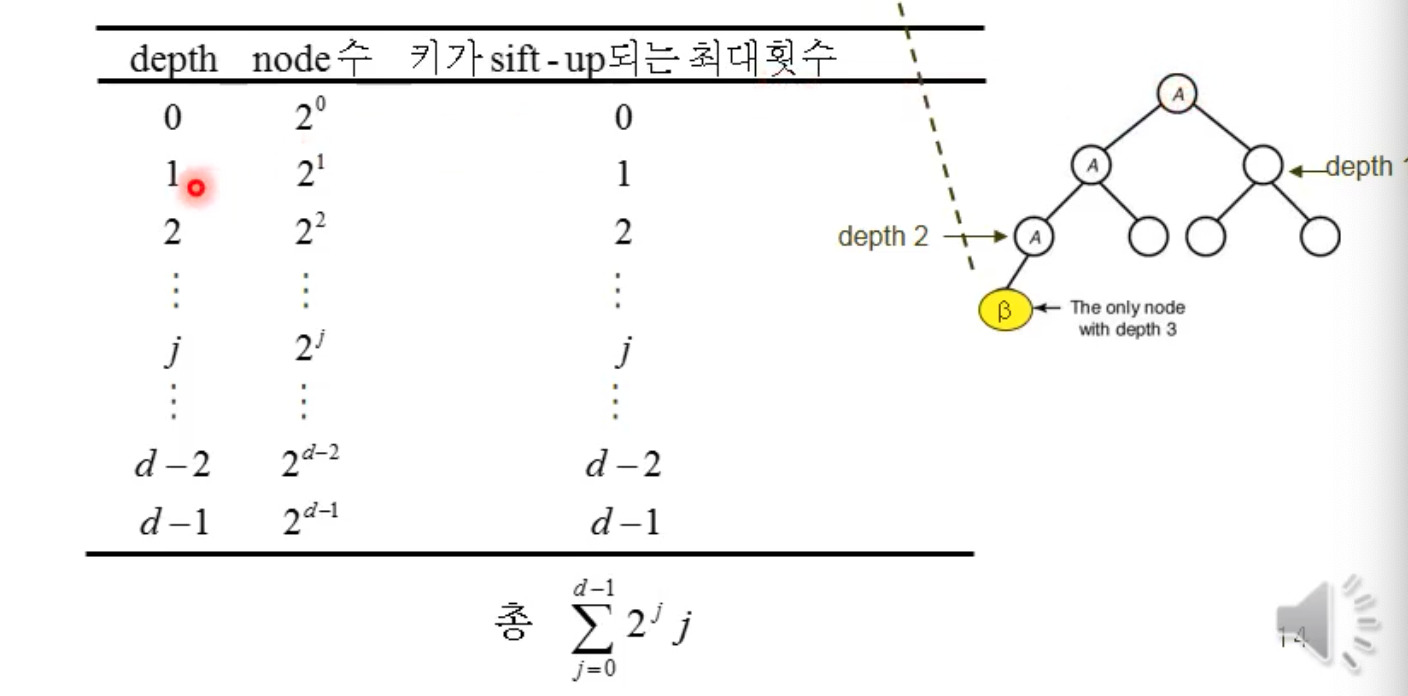시간 복잡도 계산

해당 depth에서 올라갈 수 있는 지에 대해서 횟수로 계산해서 표로 나타낸 것이다.

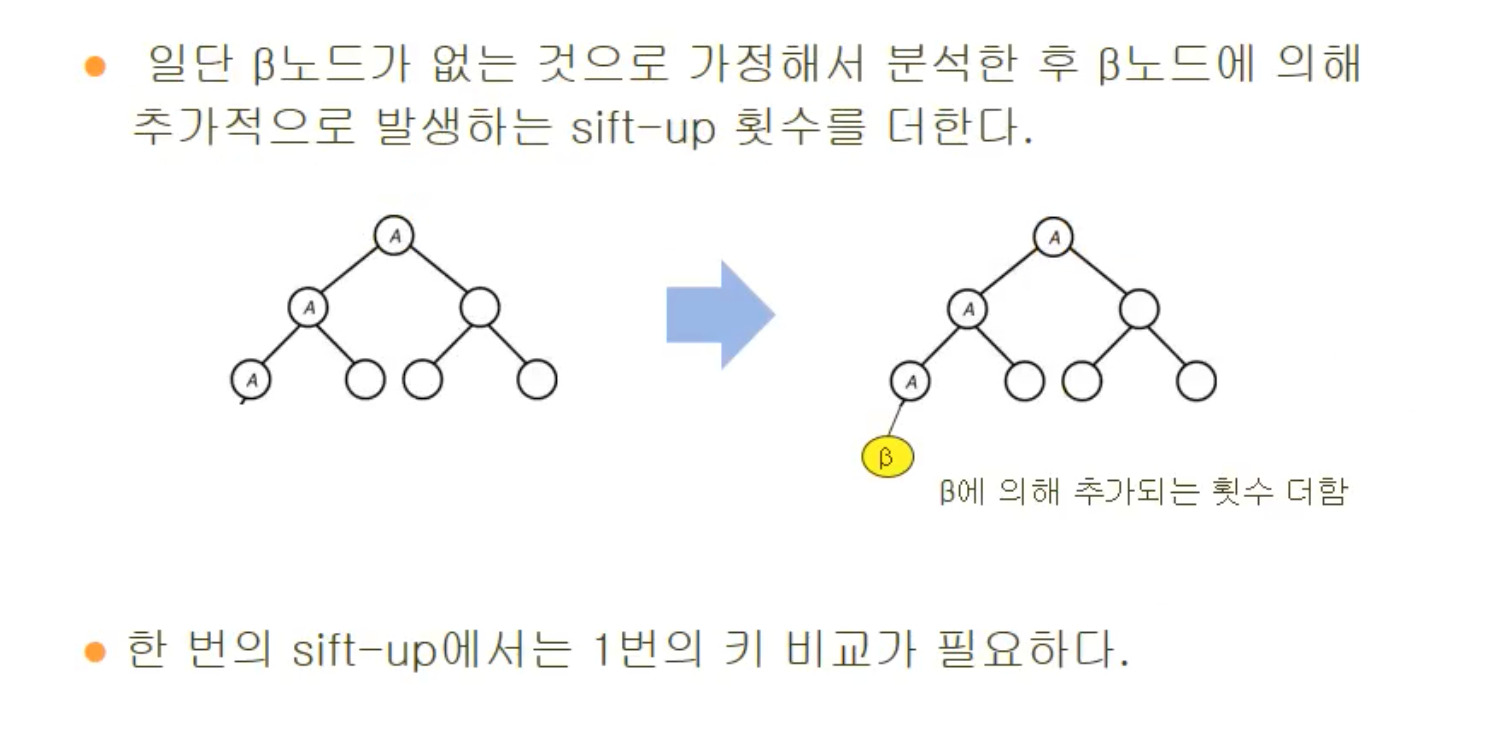
• beta가 없다 생각했을 때 nlogn-2n+2
• 만약 있다면 d만큼의 비교가 추가적으로 발생하므로 logn을 더해줌
• sift up은 올라갈 때마다 1번의 비교

Sift down

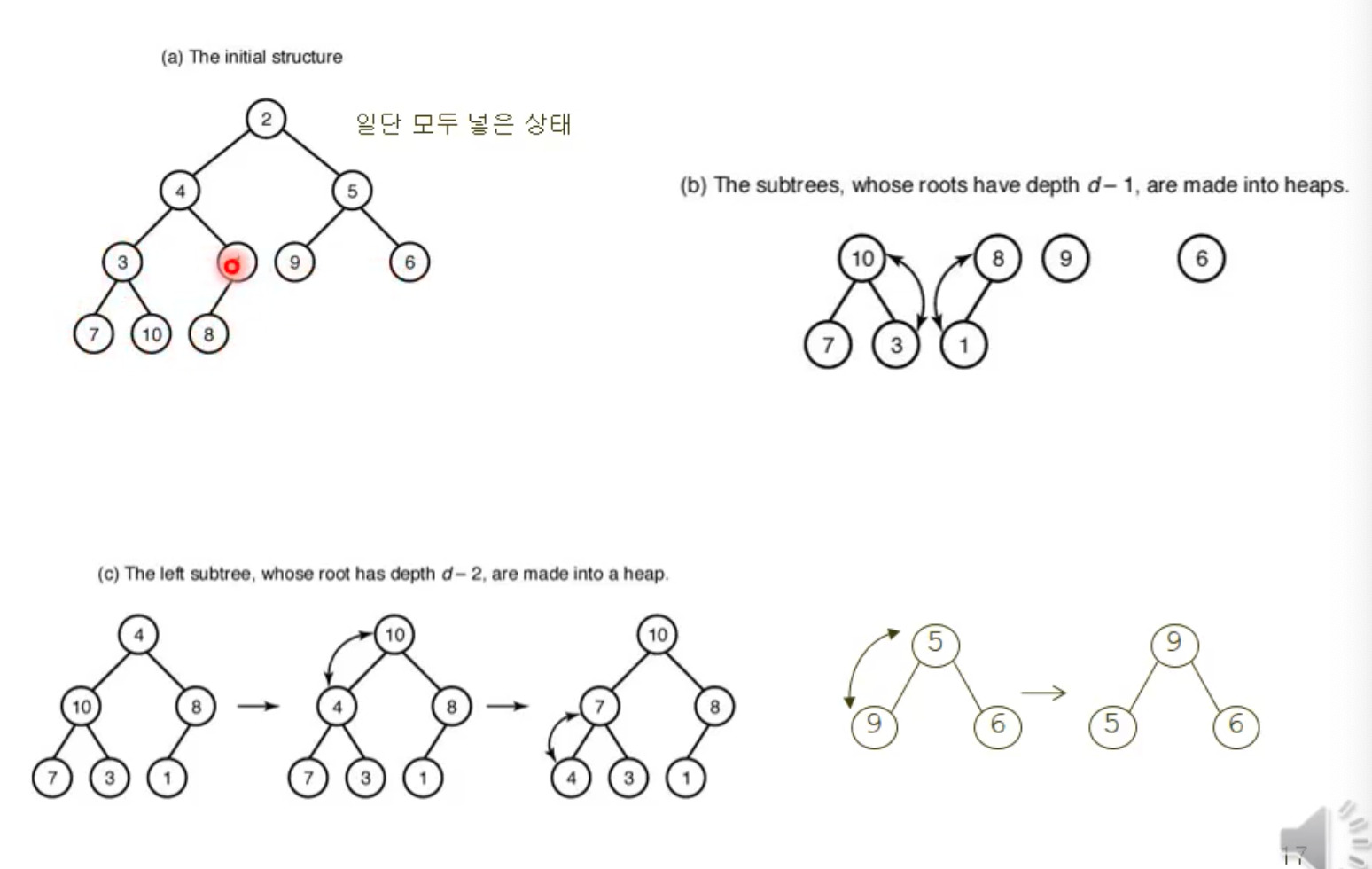
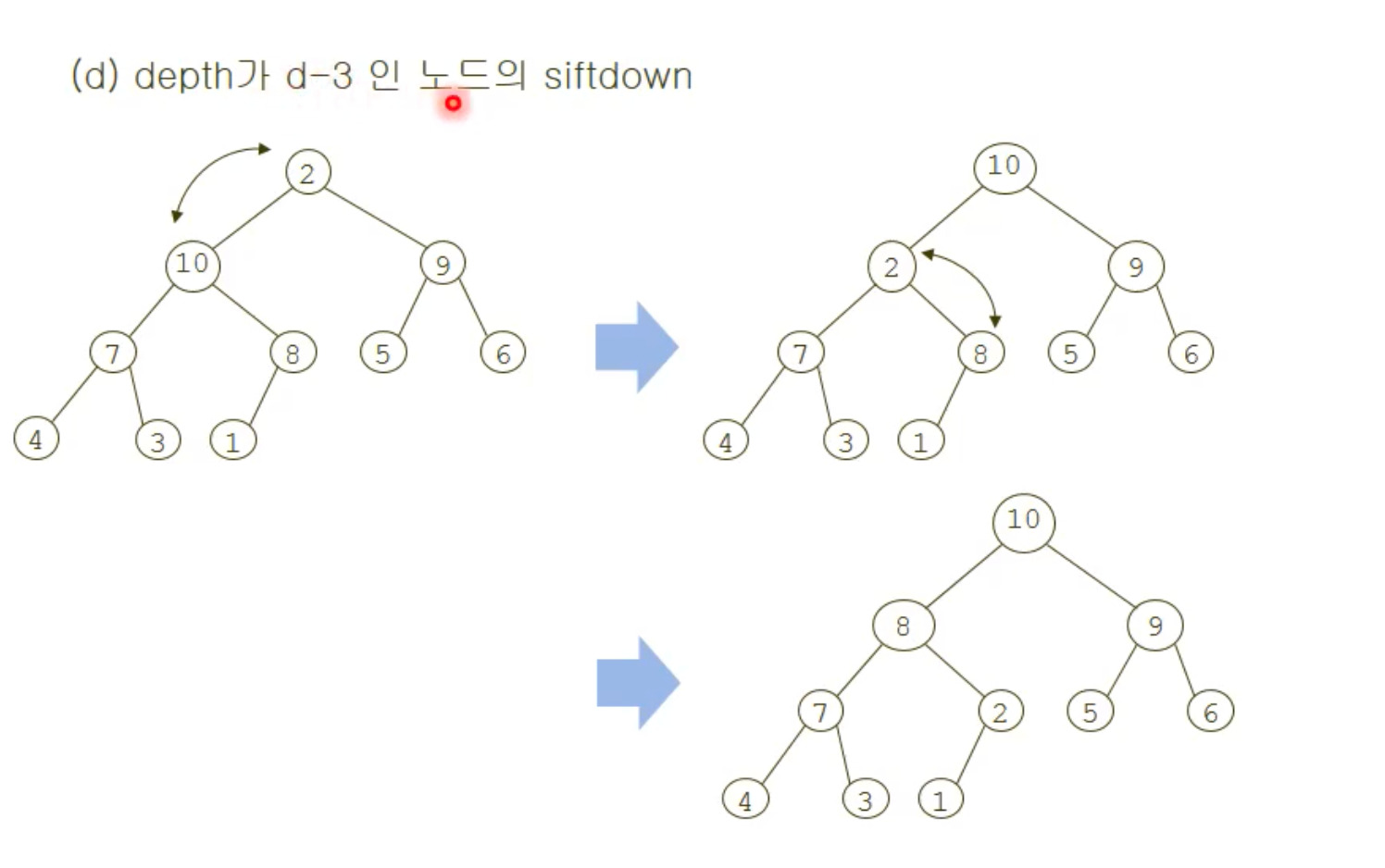
쉽게 얘기하면 뭐다? 깊은 depth부터 올라오면서 siftdown을 하는 것

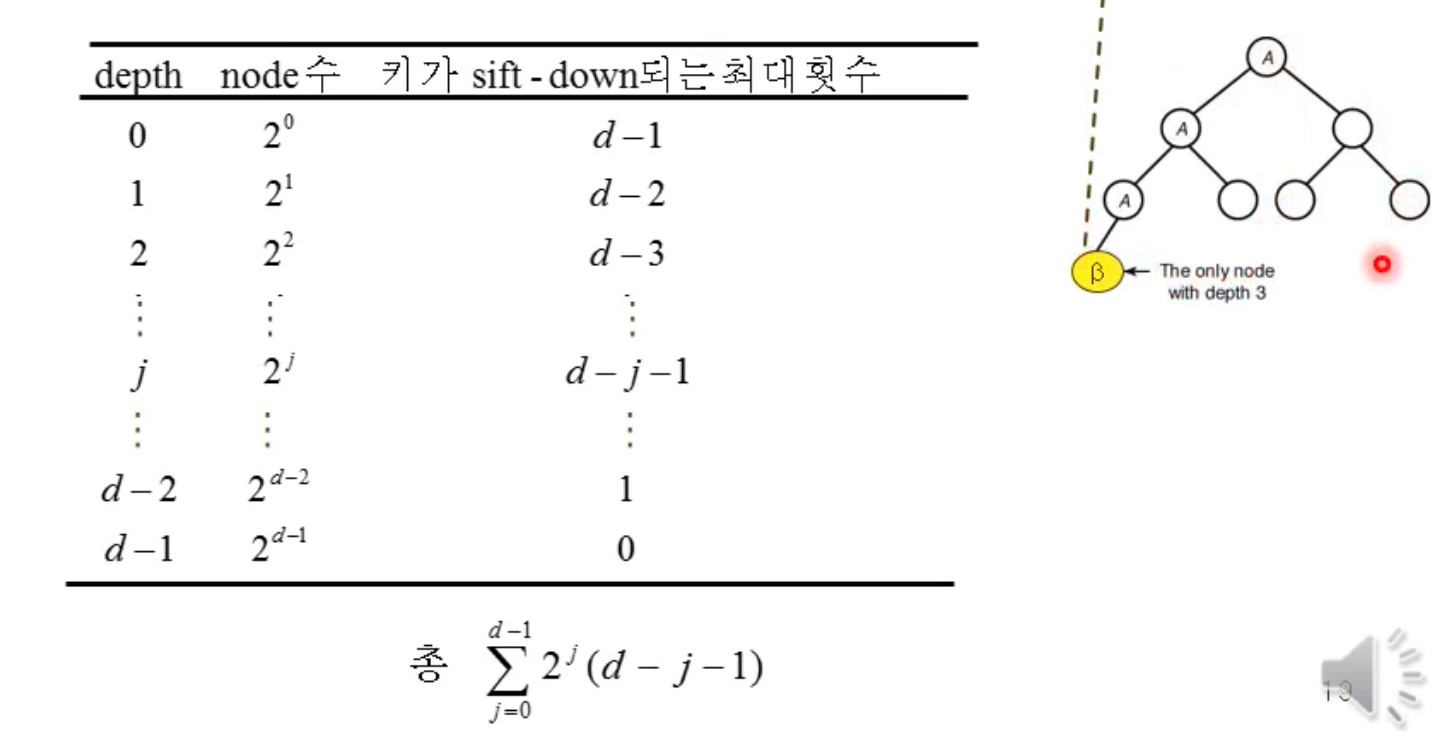Sift down 방법 시간 복잡도

해당 depth에서 아래로 내려갈 때, 필요한 비교 연산의 횟수를 나타낸 것이다. 오른쪽 그림에서 d가 3인 것을 기억하자.

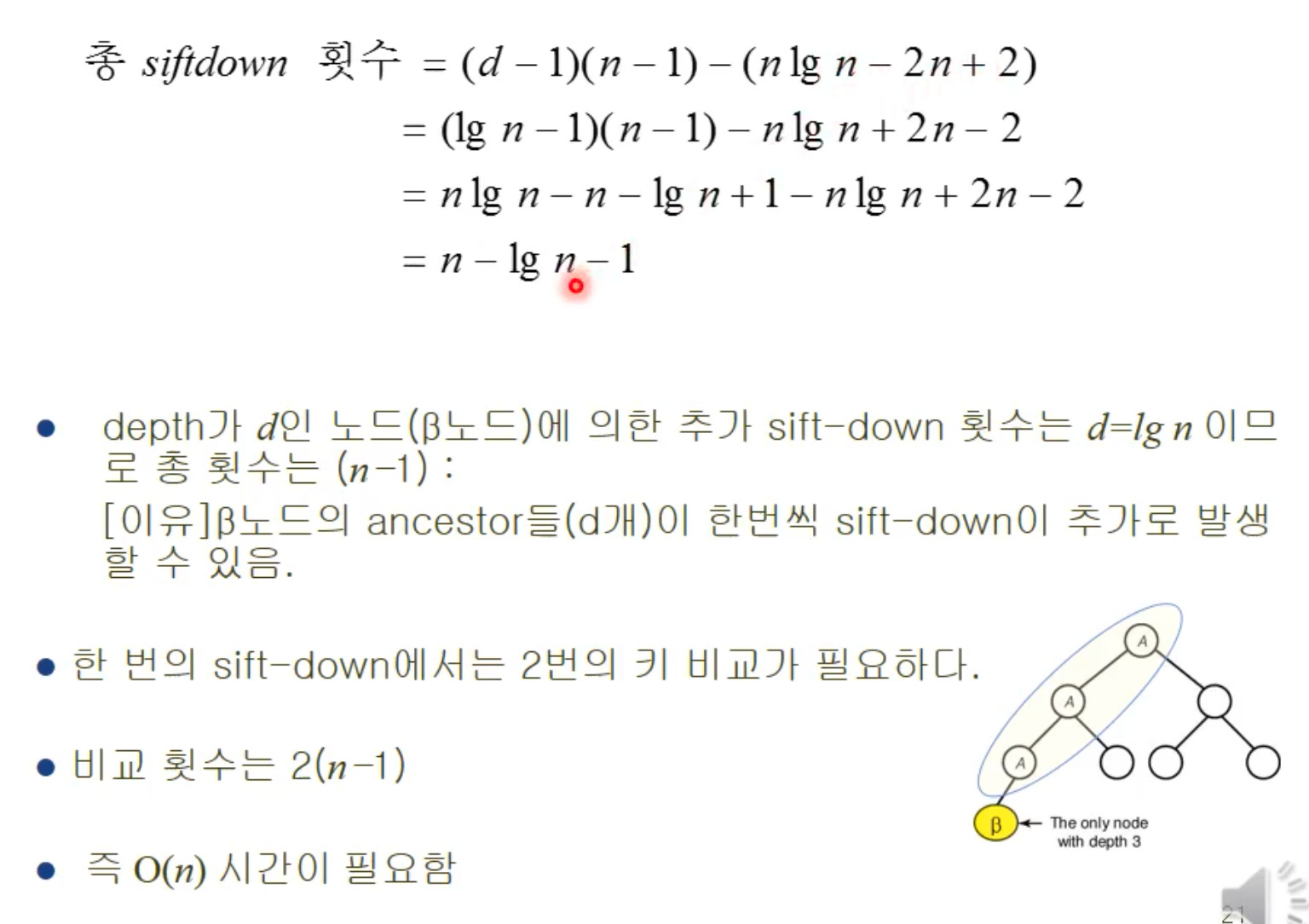
자 이렇게 구한 상태에서 beta 추가된 연산을 더해준다. beta가 추가됨에 따라, 상위 depth에 연결된 노드들에 대해 다시 sift down을 수행해야 한다. (d번)

최종적으로 n-logn-1+logn = n-1번의 siftdown이 발생한다.

그런데, siftdown에서는 2번의 비교연산이 발생하므로 총 비교 횟수는 2(n-1)이다.

즉 O(n), 상수 시간에 비교가 가능하다.

Heap 정렬의 공간 복잡도

• 제자리 정렬 알고리즘인가?
  • 즉, 입력값 이외의 추가적인 공간이 필요한가?
  • ㄴㄴ 필요없음
  • 배열로 구현한 경우 제자리 정렬 알고리즘임

Heap 정렬의 시간 복잡도

void heapsort(int b, heap& H){
    makeheap(n, H); // 2(n-1) 방법 2
    removekeys(n, H, H.S); // 2nlogn-4n+4
}

makeheap은 배웠으니 Remove keys에 대해 알아보자.

Remove keys

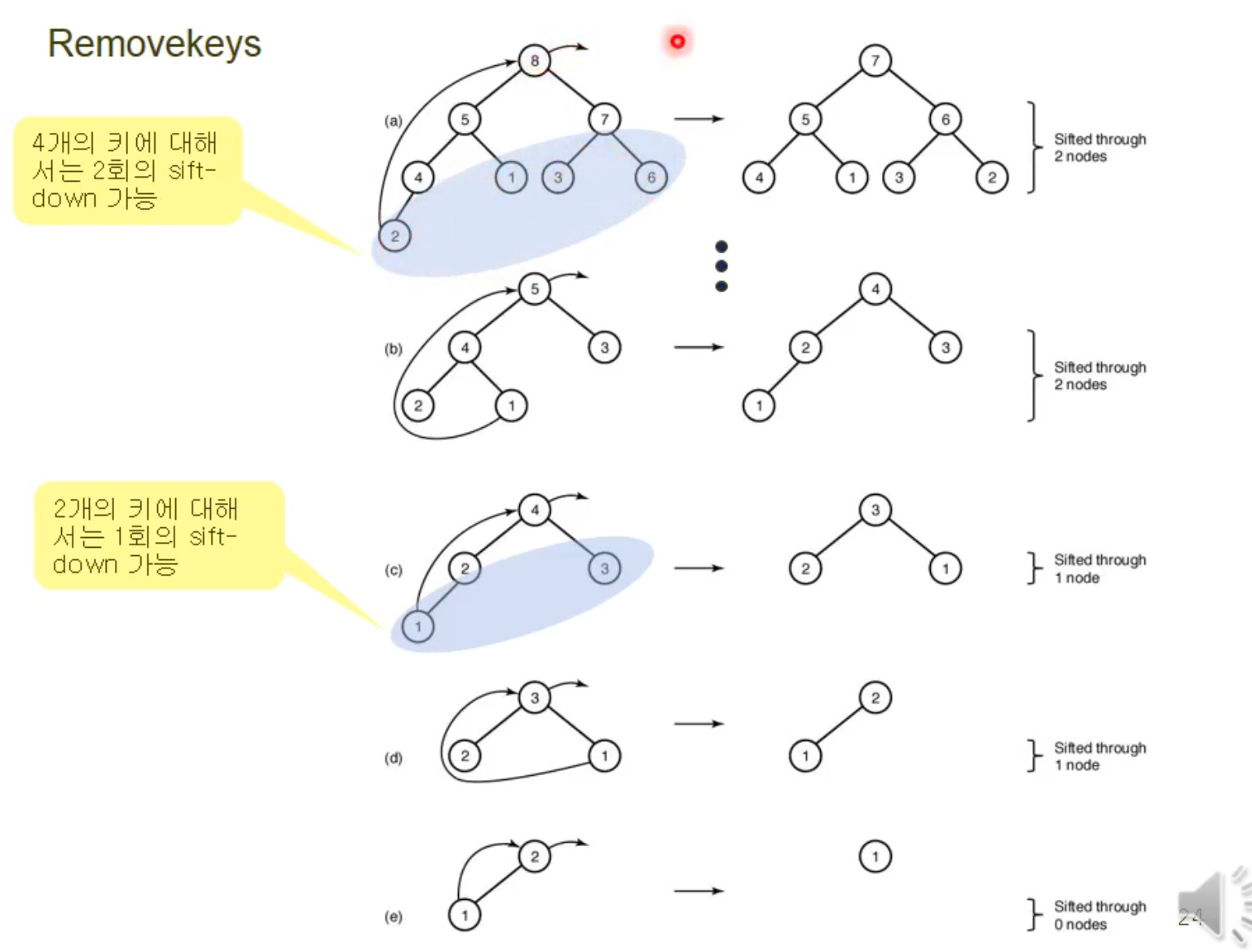removekeys

• 핵심은, 맨위의 key가 날아간 이후에 맨 아래에 있는 원소가 그 자리를 대체하게 되는데, 그럴 때마다 sift down이 이루어져야 한다는 사실이다.
• 그럼 그 siftdown이 몇번이 일어나는지 안다면 시간 복잡도를 구할 수 있다.

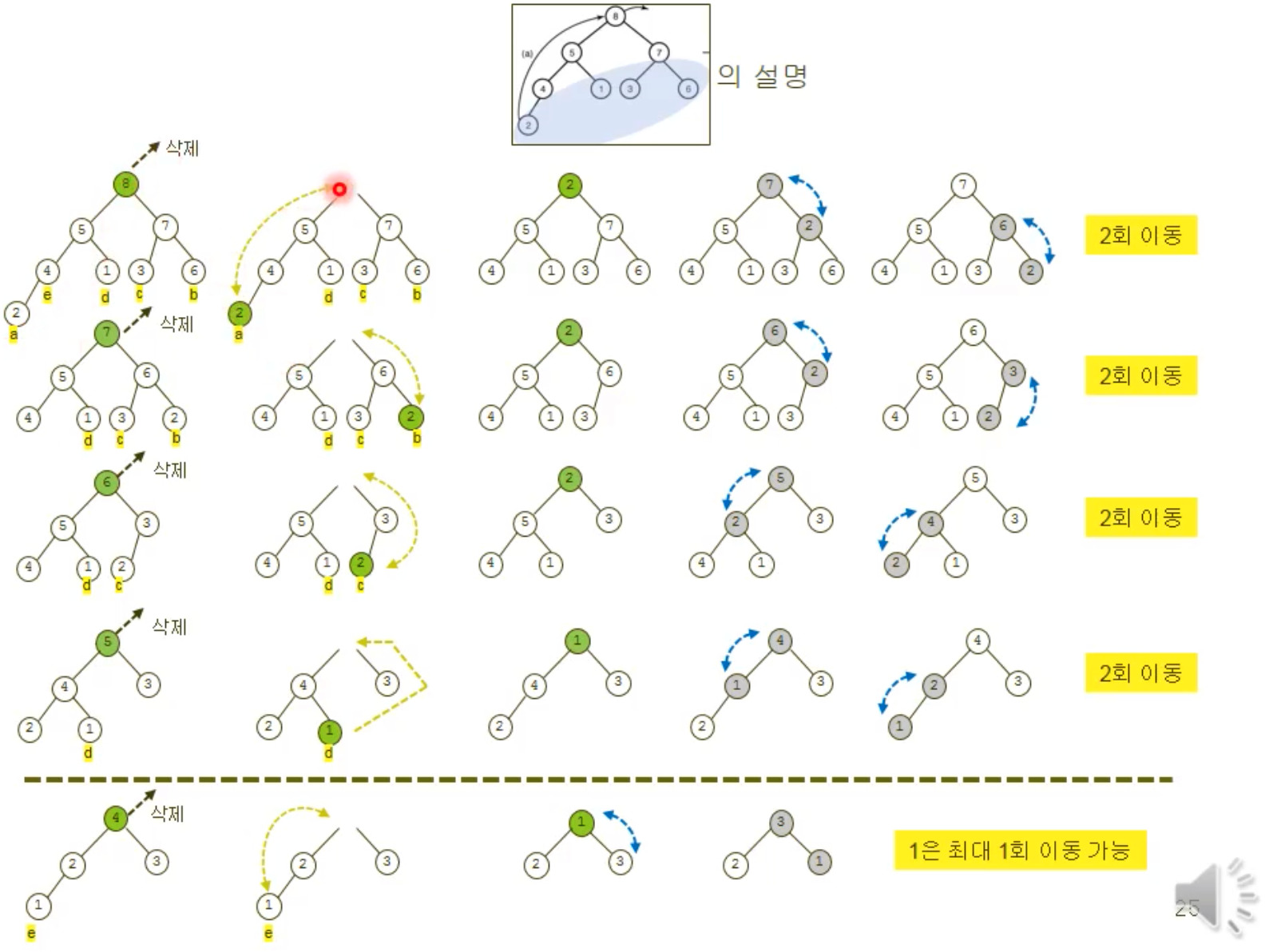depth 2에 있는 원소의 siftdown 횟수 결과..!

좀 토나오니까 이제 결과만 알고 넘어가자.

Heap, Quick, Merge

|알고리즘|비교횟수|추가저장장소|

:—:--------	:—:--------	:----:------------
합병정렬	W/A = O(nlogn)	O(n) 여분 공간 필요
퀵 정렬	W = O(n^2) A = O(nlogn)	O(logn) 재귀호출을 하는 공간 (사실 무시해도 됨)
힙 정렬	W/A = O(nlogn)	제자리 정렬

Radix Sort

Key가 비교가 안되는 경우 어떻게 해야할까? 이럴때 사용할 수 있는 비교가 아닌 정렬 방법이 있다.

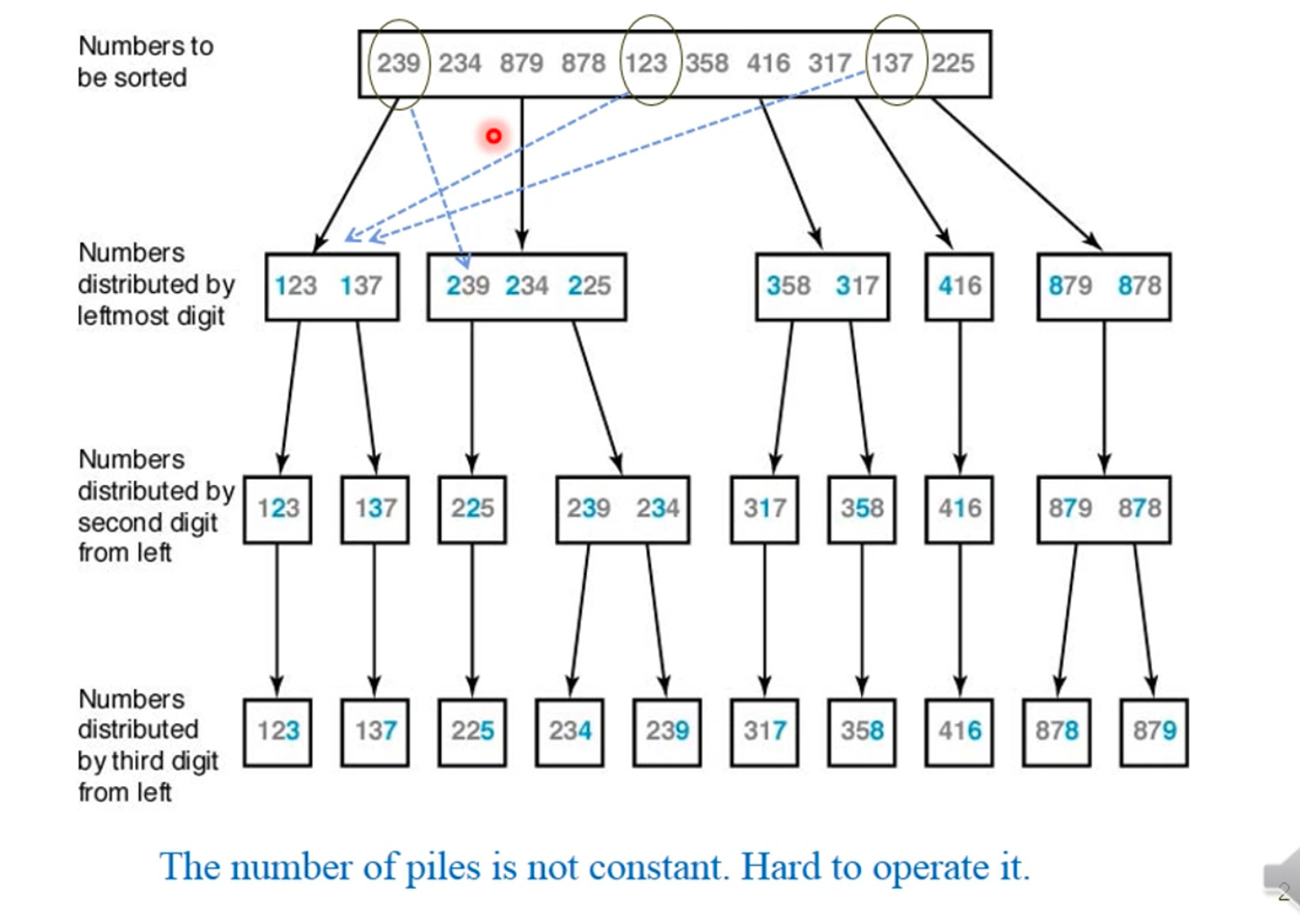왼쪽에서 오른쪽 자리순으로 정렬

약간 모으는 느낌이 강하다. 이게 뭐냐면, 백의 자리, 십의 자리, 일의 자리 순으로 정렬을 진행하는 것이다.

근데 위의 문제가 뭐냐면, 백의 자리를 묶은 다음에 그다음 단계로 가는데 있어서 각각의 pile에서 십의 자리를 나누고 있다는 것이다.

즉, 123, 137에서도 십의자리를 반영하여 123 | 137로 나누고, 239, 234, 225에서도 225 | 234, 239로 나누게 되어서 pile의 수가 급격하게 늘어난다.

이러한 문제를 해결하려면 오른쪽에서 왼쪽으로 가면된다. 그리고 각 자리수가 나올 수 있는 bucket을 만들어 관리하면 해결된다.

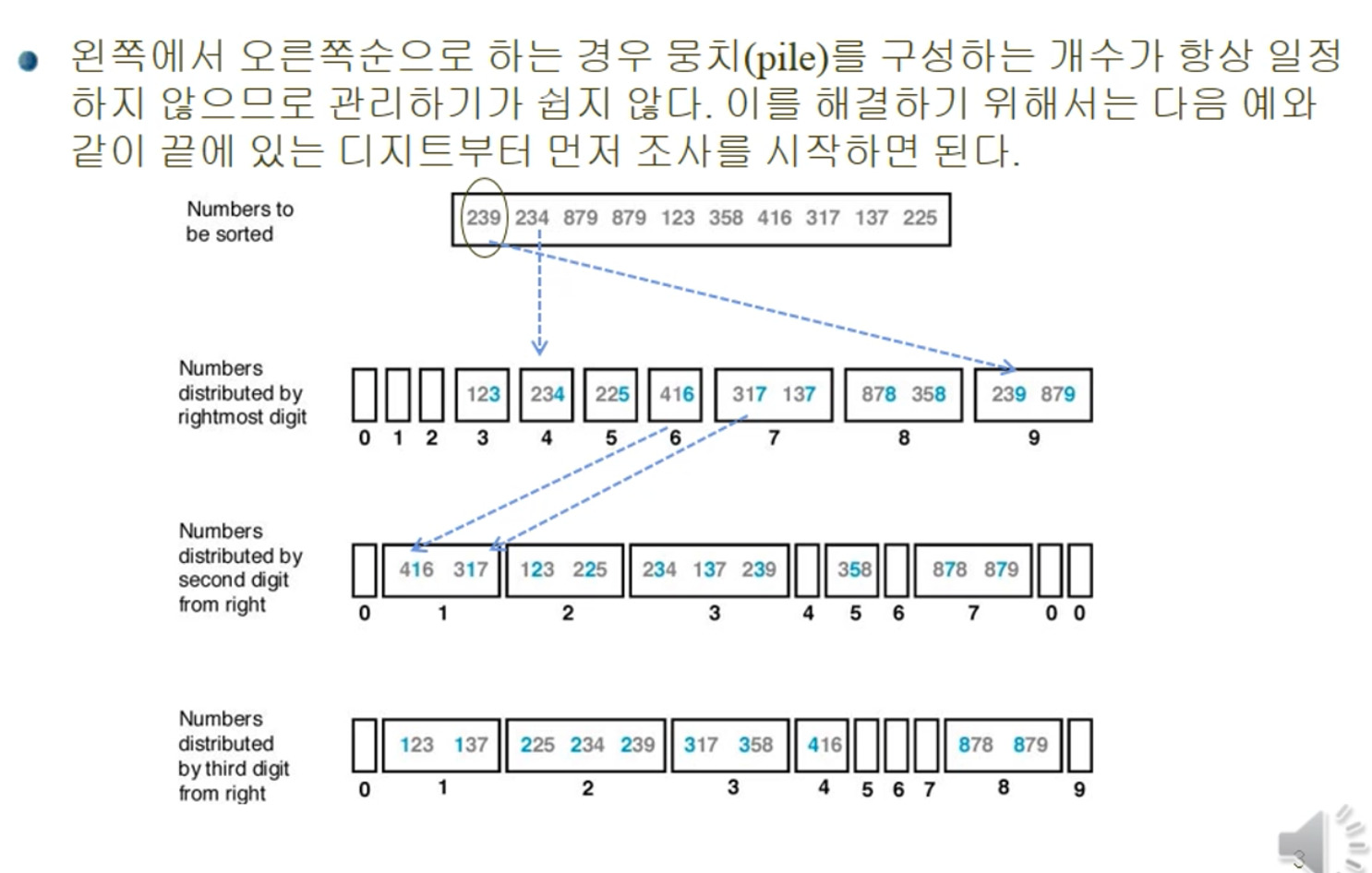오른쪽에서 왼쪽으로

순서는 다음과 같다.

1. 일의 자리를 기준으로 bucket에 담는다.
2. 순서대로 배열화 한다.
3. 십의 자리를 기준으로 bucket에 담는다.
4. 배열화 한다.
5. 백의 자리를 기준으로 bucket에 담는다.
6. 배열화 한다.

굉장히 간단하다..

• 연산

  • 분배
    • 현재 배열에 있는 수를 Bucket에 담는 연산 O(n)
  • 병합(coalesce)
    • bucket에 있는 것을 변환함 O(10)
    • 링크드 리스트로 붙여버림

• 시간 복잡도

  • 자리수 * (분배(n) + 병합(10)) = O(자리수(d)*개수n)

• 공간 복잡도

  • 추가적으로 bucket에 저장할 수 있어야 하므로 O(n)

자, 그러면 만약 16개(n)의 수가 있다면 몇개의 자리수(d)가 필요할까? 보통 logn개면 충분하다. 그러니 16개의 수를 정렬하는데 걸리는 시간은 16*log16 = 64이다.

사실 정확하게 시간 복잡도를 나타내면 다음과같다.

T(n) = d * (n+k)

• d : 자리수
• n : 개수
• k : 진법에 따른 범위

위상 정렬 (Topological Sort)

순서 정하기..!

DFS에 코드를 추가하는 방향으로 구현이 가능하다.