Vector Representation

좌표계의 회전 변환

i번째에서 정의된 좌표계는, 내가 원하는 global 좌표계에서 좌표로 다음과 같은 관계를 갖는다.

\\begin{bmatrix} x_p\\ y_p \\end{bmatrix};=; \\begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta\\ \\end{bmatrix} \\begin{bmatrix} x_p^i\\ y_p^i \\end{bmatrix}

이 행렬을 A라 정의하자.

A^i;=;\begin{bmatrix} cos\theta & -sin\theta\\ sin\theta & cos\theta\\ \\end{bmatrix}

위치 벡터의 표현

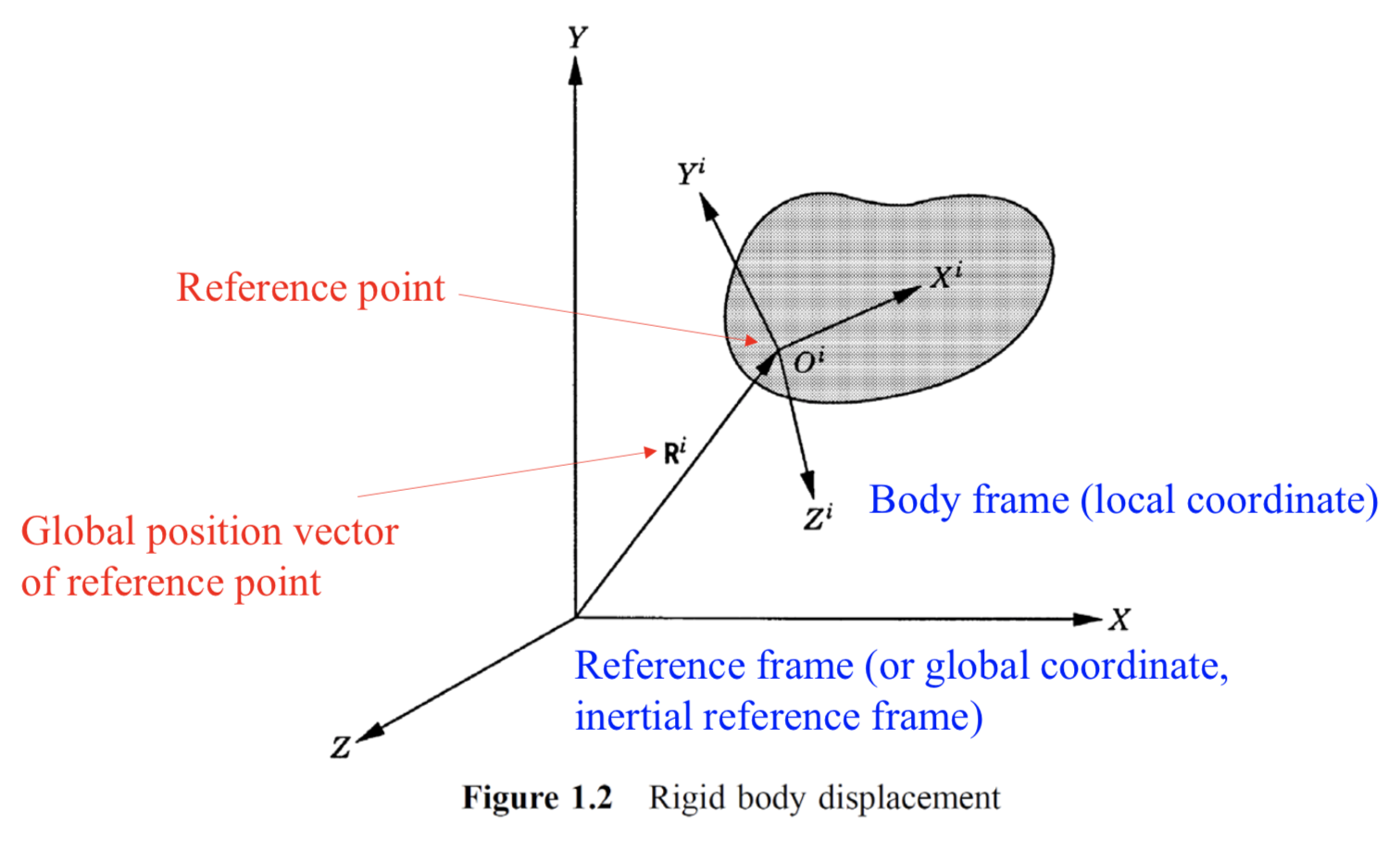
다음과 같이 global 좌표계가 있고, 특정 body에서 정의된 좌표계가 있을 때, 우리는 이 두 좌표계를 변환할 필요가 있다. global 좌표계에서 body의 움직임을 알고 싶다. 강체라 가정하고, body의 좌표계에서 중심점이 되는 곳을 우리는 reference point 라 부른다. 또 그곳에서 정의되는 좌표계를 body frame, local coordinate 라 한다. 그리고 global 좌표계의 중심이 되는 곳을 reference frame 이라 부를 것이다. 이 두좌표계를 변환하는 관계식은 다음과 같다.

$$overset\to {r_p}^i;=;{\overrightarrow{R}}^i;+;{\overrightarrow{u_p}}^i$$

이 표기법을 말로 정의해보면, global 좌표계에서 표현된 p점의 벡터 는, reference point까지의 벡터 와 reference point로 부터 global 좌표계에서 표현된 특정 위치의 벡터 를 더한 것이다. 라는 의미이다. 이 때, reference point로 부터 global 좌표계에서 표현된 특정 위치의 벡터는 local coordinate 로 부터 global coordinate 로 회전 변환 한 것이므로,

$$overset\to {r_p}^i;=;{\overrightarrow{R}}^i;+;A^i{\overrightarrow{\stackrel{-}{u_p}}}^i$$

여기서 맨 오른쪽에 표현된 term은, local coordinate에서 표현된 특정 좌표이다.

$$\begin{gathered} overset\to {\stackrel{-}{u_p}}^i;=; \\ beginbmatrix{\stackrel{-}{x_p}}^i \\ {\stackrel{-}{y_p}}^i \\ endbmatrix \end{gathered}$$

속도 벡터의 표현

위치벡터를 미분하면, 얻을 수 있다.

$$overset\to {r_p}^i;=\frac{d}{dt}{\overrightarrow{r_p}}^i;=;;\stackrel{\cdot }{{\overrightarrow{R}}^i};+;\stackrel{\cdot }{A^i}{\overrightarrow{\stackrel{-}{u_p}}}^i;+;A^i\stackrel{\cdot }{{\overrightarrow{\stackrel{-}{u_p}}}^i}$$

여기서 의미를 파악해보면, 시간에 흐름에 따라, Rigid body assumption 에 의해 local coordinate 안에서 p점의 속도는 0이다. 따라서 마지막 항은 0이다.

$$overset\to {r_p}^i;=\frac{d}{dt}{\overrightarrow{r_p}}^i;=;;\stackrel{\cdot }{{\overrightarrow{R}}^i};+;\stackrel{\cdot }{A^i}{\overrightarrow{\stackrel{-}{u_p}}}^i$$

여기서 행렬 미분을 생각해보면, A는 theta 만의 함수이므로 이녀석을 시간 t에 대해 미분하면, chain rule 에 의해,

$$overset\cdot A^i;=;\frac{d}{dt}{A}^i({\theta }^i);=;\frac{d{\theta }^i}{dt}(\frac{d}{d{\theta }^i}{A}^i);=;\stackrel{\cdot }{{\theta }^i}{A}^i\_,\theta$$

이렇게 표현되고, A를 theta에 대해 미분한 행렬은,

A^i\_{,\theta};=;\begin{bmatrix} -sin\theta^i & -cos\theta^i\\ cos\theta^i & -sin\theta^i\\ \\end{bmatrix}

Transform to Cross product form

결과적으로, 강체에서 속도 벡터는,

$$overset\cdot {\overrightarrow{r_p}}^i;=\stackrel{\cdot }{{\overrightarrow{R}}^i};+;\stackrel{\cdot }{{\theta }^i}{A}^i\_,\theta {\overrightarrow{\stackrel{-}{u_p}}}^i$$

2D에서 각속도 벡터는,

\\overset{\rightarrow}{\omega}^i;=;\overset{\cdot}{\theta^i}\hat{k};=;\[0;;;;0;;;;\overset{\cdot}{\theta^i}\]^T

이 때,

\\overset{\cdot}{\theta^i}A^i\_{,\theta} \overset{\rightarrow}{\overset{-}{u_p} }^i;=; \\overset{\cdot}{\theta^i} \\begin{bmatrix} -sin\theta^i & -cos\theta^i\\ cos\theta^i & -sin\theta^i\\ \\end{bmatrix} \\begin{bmatrix} \\overset{-}{x_p}^i\\ \\overset{-}{y_p}^i\\ \\end{bmatrix} ;=; \\overset{\cdot}{\theta^i}\begin{bmatrix} -\overset{-}{x_p}^isin\theta^i-\overset{-}{y_p}^icos\theta^i\\ \\overset{-}{x_p}^icos\theta^i-\overset{-}{y_p}^isin\theta^i \\end{bmatrix}

로 정리될 수 있다. 여기서 Up 벡터는 다음과 같이 표현 될 수 있다.

\\overset{\rightarrow}{ {u_p} }^i; =;A^i\overset{\rightarrow}{\overset{-}{u_p} }^i;=; \\begin{bmatrix} cos\theta^i & -sin\theta^i\\ sin\theta^i & cos\theta^i\\ \\end{bmatrix} \\begin{bmatrix} \\overset{-}{x_p}^i\\ \\overset{-}{y_p}^i\\ \\end{bmatrix} ;=;\begin{bmatrix} \\overset{-}{x_p}^icos\theta^i-\overset{-}{y_p}^isin\theta^i\\ \\overset{-}{x_p}^isin\theta^i+\overset{-}{y_p}^icos\theta^i \\end{bmatrix} ;=; \\begin{bmatrix} u_x^i\\ u_y^i\\ \\end{bmatrix}

각속도 백터와 Up 벡터를 내적하면,

\\overset{\rightarrow}{\omega}^i\times\overset{\rightarrow}{ {u_p} }^i;=; \\begin{vmatrix} \\hat{i} & \hat{j} & \hat{k} \\ 0 & 0 & \overset{\cdot}{\theta^i}\\ u_x^i & u_y^i & 0 \\end{vmatrix} \\ ;\\ ;=; \\begin{vmatrix} 0 & \overset{\cdot}{\theta^i} \\ u_y^i & 0 \end{vmatrix}\hat{i} -\begin{vmatrix} 0 & \overset{\cdot}{\theta^i} \\ u_x^i & 0 \end{vmatrix}\hat{j} +\begin{vmatrix} 0 & 0 \\ u_x^i & u_y^i \end{vmatrix}\hat{k}\\ ;\\ ;=;-\overset{\cdot}{\theta^i}u_y^i\hat i;+;\overset{\cdot}{\theta^i}u_x^i\hat j \\ ;\\ ;\\

이 식을 행렬식으로 표현하면,

\\overset{\cdot}{\theta^i}\begin{bmatrix} -u_y^i\\ u_x^i\\ \\end{bmatrix};=; \\overset{\cdot}{\theta^i}\begin{bmatrix} -\overset{-}{x_p}^isin\theta^i-\overset{-}{y_p}^icos\theta^i\\ \\overset{-}{x_p}^icos\theta^i-\overset{-}{y_p}^isin\theta^i \\end{bmatrix};=;\overset{\cdot}{\theta^i}A^i\_{,\theta} \overset{\rightarrow}{\overset{-}{u_p} }^i

따라서,

$$overset\cdot {\theta }^i{A}^i\_,\theta {\overrightarrow{\stackrel{-}{u_p}}}^i;=;{\overrightarrow{\omega }}^i\times {\overrightarrow{u_p}}^i$$

Summary

결론적으로 속도 벡터는 다음과 같이 표현된다.

$$overset\to {r_p}^i;=\stackrel{\cdot }{{\overrightarrow{R}}^i};+;\stackrel{\cdot }{{\theta }^i}{A}^i\_,\theta {\overrightarrow{\stackrel{-}{u_p}}}^i;=;\stackrel{\cdot }{{\overrightarrow{R}}^i}+;{\overrightarrow{\omega }}^i\times {\overrightarrow{u_p}}^i$$

가속도 벡터의 표현

\\overset{\cdot \cdot}{\overset{\rightarrow}{r_p}^i} ;=;{d\over dt }\overset{\cdot}{\overset{\rightarrow}{r_p}^i};=; {d\over dt}\[\\overset{\cdot}{\overset{\rightarrow}{R}^i};+;\overset{\cdot}{\theta^i}A^i\_{,\theta} \overset{\rightarrow}{\overset{-}{u_p} }^i\]

정리하면,

\\overset{\cdot \cdot}{\overset{\rightarrow}{r_p}^i};=; \\overset{\cdot \cdot}{\overset{\rightarrow}{R}^i} -(\overset{\cdot}{\theta^i})^2A^i \overset{\rightarrow}{\overset{-}{u_p} }^i +\overset{\cdot \cdot}{\theta^i}A^i\_{,\theta} \overset{\rightarrow}{\overset{-}{u_p} }^i \\ ;\\ ;=; \\overset{\cdot \cdot}{\overset{\rightarrow}{R}^i}+ \[\\overset{\rightarrow}{\omega}^i\times(\overset{\rightarrow}{\omega}^i\times\overset{\rightarrow}{ {u_p} }^i)\] +\[\\alpha^i \times\overset{\rightarrow}{ {u_p} }^i\]

여기서 alpha는,

\\alpha^i;=;\[0;;;;0;;;;\overset{\cdot \cdot}{\theta^i}\]^T

이다.