데이터의 두 변수간 선형관계를 나타내는 척도에 대해서 알아본다.

선형관계

두 변수의 관계를 알아보는 것은 매우 중요하다. 어떠한 연관성을 통하여 유의미한 정보를 이끌어 낼 수 있기 때문이다. 이러한 선형관계를 알아내는 척도는 3가지 정도가 알려져 있다.

공분산(Covarience)

o p er a t or nam e C o v (X, Y) = E ((X - μ) (Y - ν)^{⊤})

공분산을 직관적으로 이해하면 다음과 같다. 식을 보면, 결국 X에서 X의 평균을 빼고, Y에서 Y의 평균을 뺀뒤 곱한 것들을 모두 더한뒤 데이터의 개수로 나누는 것이다. 그렇다면 안에 있는 $(X - μ) (Y - ν)$ 만 확인해보자.

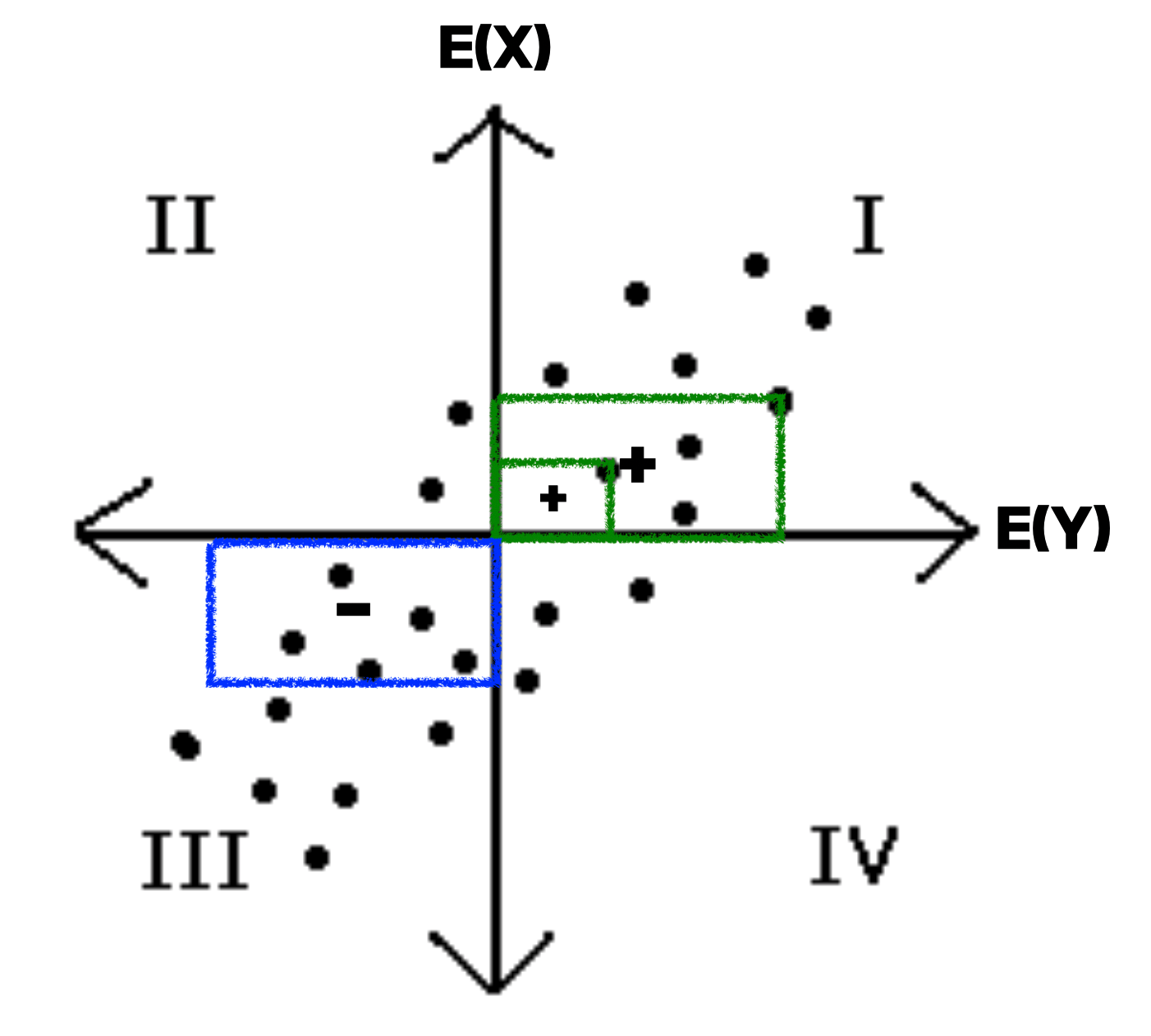위와 같은 그림이 된다.

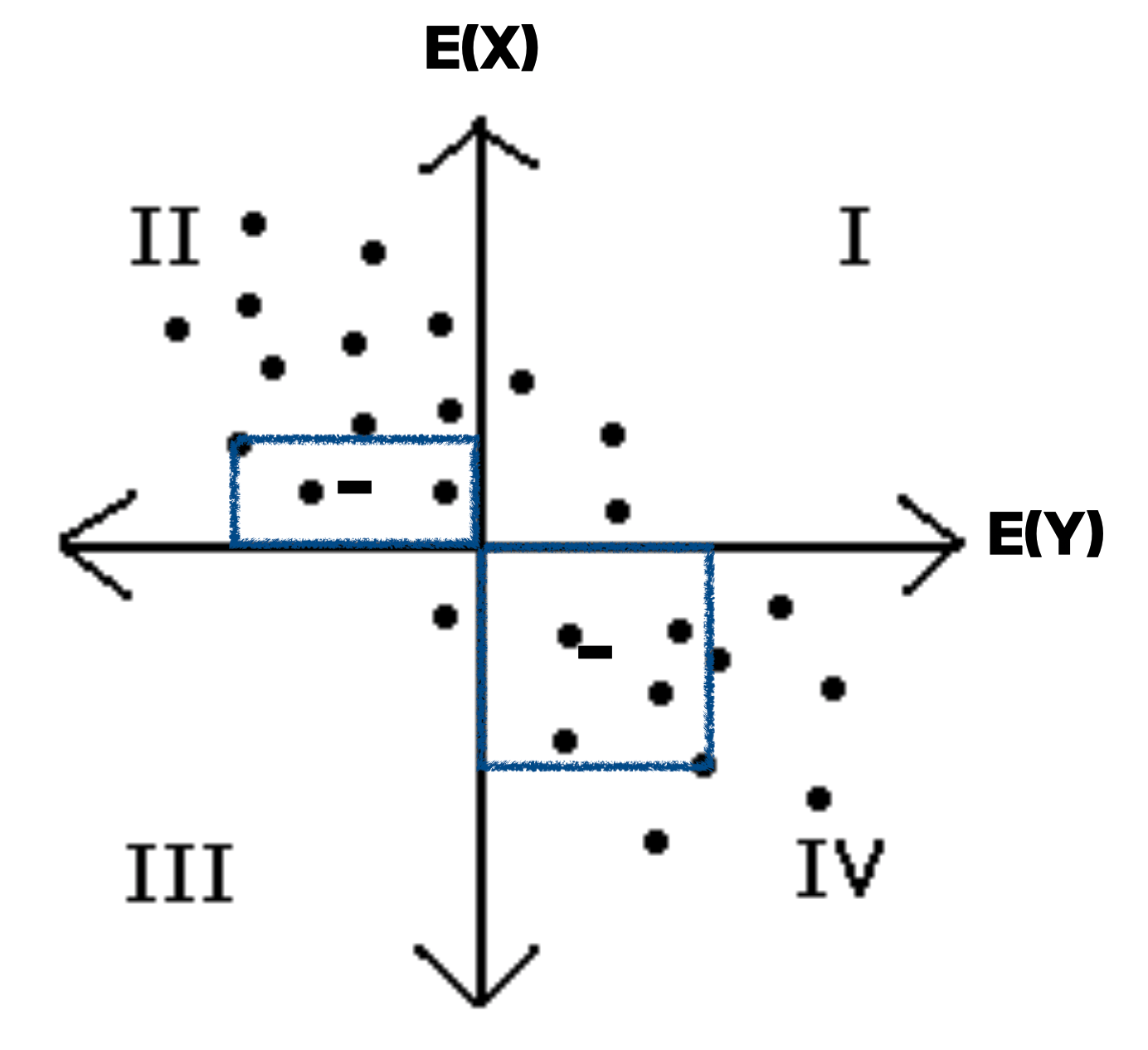
이러한 특징 때문에, 결과적으로 양의 상관관계를 가지는 경우는 +, 음의 상관관계는 -가 된다.

결론부터 말하자면 x, y축에 대해 평행한 직선에 대해 대칭이면 모두 0이 나온다. 실제로 그림을 그려보고 위의 작업을 해보도록 하자.

상관 계수는 위의 값을 정규화했다고 보면 된다. 결과적으로 -1~+1의 값으로 만들어 보다 수치적으로 정확히 판단할 수 있다. 이는 벡터의 내적과 동일한 연산이다.

공분산 행렬은 다변수 데이터의 공분산을 나타낸다. 이는 다음과 같이 표현된다.

\\begin{aligned} \\operatorname{Cov}(X) &= \operatorname{E}((X-\mu)(X-\mu)^\top) \\ &= \begin{bmatrix} \\operatorname{Cov}(X_1, X_1) & \operatorname{Cov}(X_1, X_2) & \cdots & \operatorname{Cov}(X_1, X_n) \\ \\operatorname{Cov}(X_2, X_1) & \operatorname{Cov}(X_2, X_2) & \cdots & \operatorname{Cov}(X_2, X_n) \\ \\vdots & \vdots & \ddots & \vdots \\ \\operatorname{Cov}(X_n, X_1) & \operatorname{Cov}(X_n, X_2) & \cdots & \operatorname{Cov}(X_n, X_n) \\end{bmatrix} \\end{aligned}