BOJ - 최소값(10868)

플래티넘5 : 세그먼트 트리 문제이다.

생각

|0|1|2|3|4|5|6| |:|:|:|:|:|:|:| |4|1|7|5|2|9|8|

입력값이 이렇게 주어진다고 생각해보자. 이 상태에서 3~6까지의 최소값을 구하는 것은, 단순한 방법으로 구해도 $O(n^2)$으로 풀 수 있다. 하지만 이러한 확인(쿼리)가 많아진다면, 급격하게 시간 복잡도가 올라간다. 따라서 이 문제에서 제시하는 m(100000) 개에 대해서 n(100000)을 모두 확인하는 방법으로 간다면 문제를 풀 수 없다.($O(n^2)$)

문제의 원인

그렇다면 어느 부분에서 연산이 많이 걸리는 지 생각해보자. 가장 큰 부분을 판단을 중복으로 한다는 것이다. 03까지의 최소값을 구하는 것과, 14까지의 최소값을 구하는 과정에는 1~3까지의 최소값을 비교하는 과정이 중복된다. 그렇다면, 처음에 주어진 index를 나누어, 그 나눈 구간에 대해 최소값을 구해놓으면 어떨까?

어떻게 나눌까?

나누겠다는 생각이 들고 난 후에는, 어떻게 하면 잘 나눌 수 있을 지에 대해 고민했다. 이 부분은 트리가 가장 용이하다. 정보를 저장하는 자료구조 중, 탐색에 있어 시간복잡도가 log이다. 나누는 방법은 생각 보다 간단하다.

Tree 구조

트리의 구조는 모양의 변화를 가지는 것이다. 우리가 보통 가지는 선형 리스트를 조금 바꾸어 생각하면 쉽게 트리 구조를 만들 수 있다.

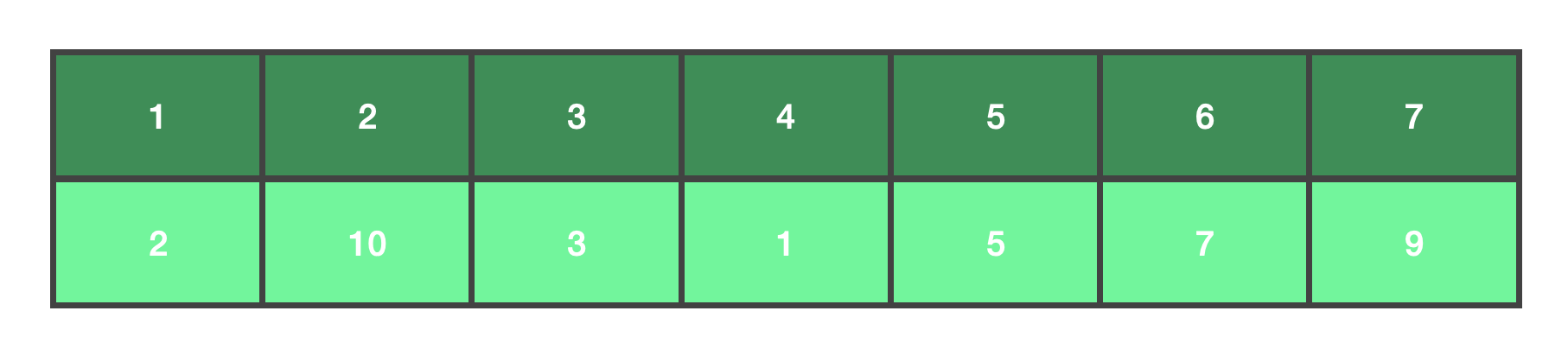
이렇게 2의 제곱수만큼의 개수를 아래쪽으로 옮기면서 쌓으면 트리 구조가 된다. 이 때, 중요한 것은 가장 위층으로 부터 아래로 내려오는데 그 index들의 관계를 아는 것이다. 잘 보면, 1에서 2, 3은 $2\times 1$, $2\times 1+1$ 과 같다. 왼쪽 트리, 오른쪽 트리로 가는 관계는 계속 일관성을 가진다.

Segment Tree

그렇다면 이번에는 이 트리 구조를 이 문제에 맞는 모양으로 바꾸어 보자. 우리는 최소값을 미리 저장하기 위해 트리구조를 사용하기로 했는데, 그 구조를 아래와 같이 만들어서 생각해보자.

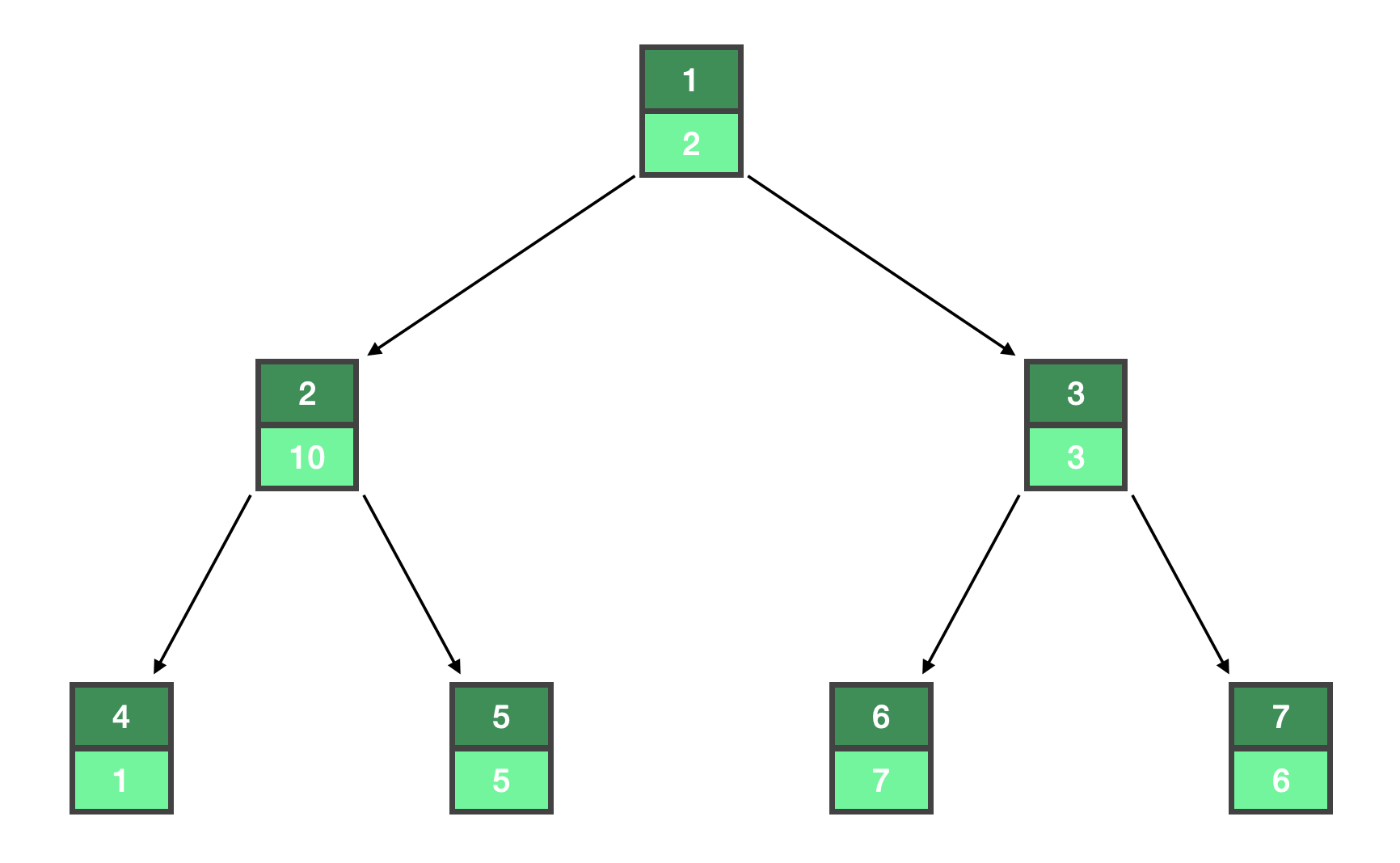
기본적인 트리구조는 같지만 추가된 변수가 있다. 그것은 index의 시작과 끝을 나타내는 startend 변수이다. 이렇게 나누었다고 가정하고, 25까지의 최소값을 얻기위해 조사해야 하는 Node의 개수를 파악해보자.

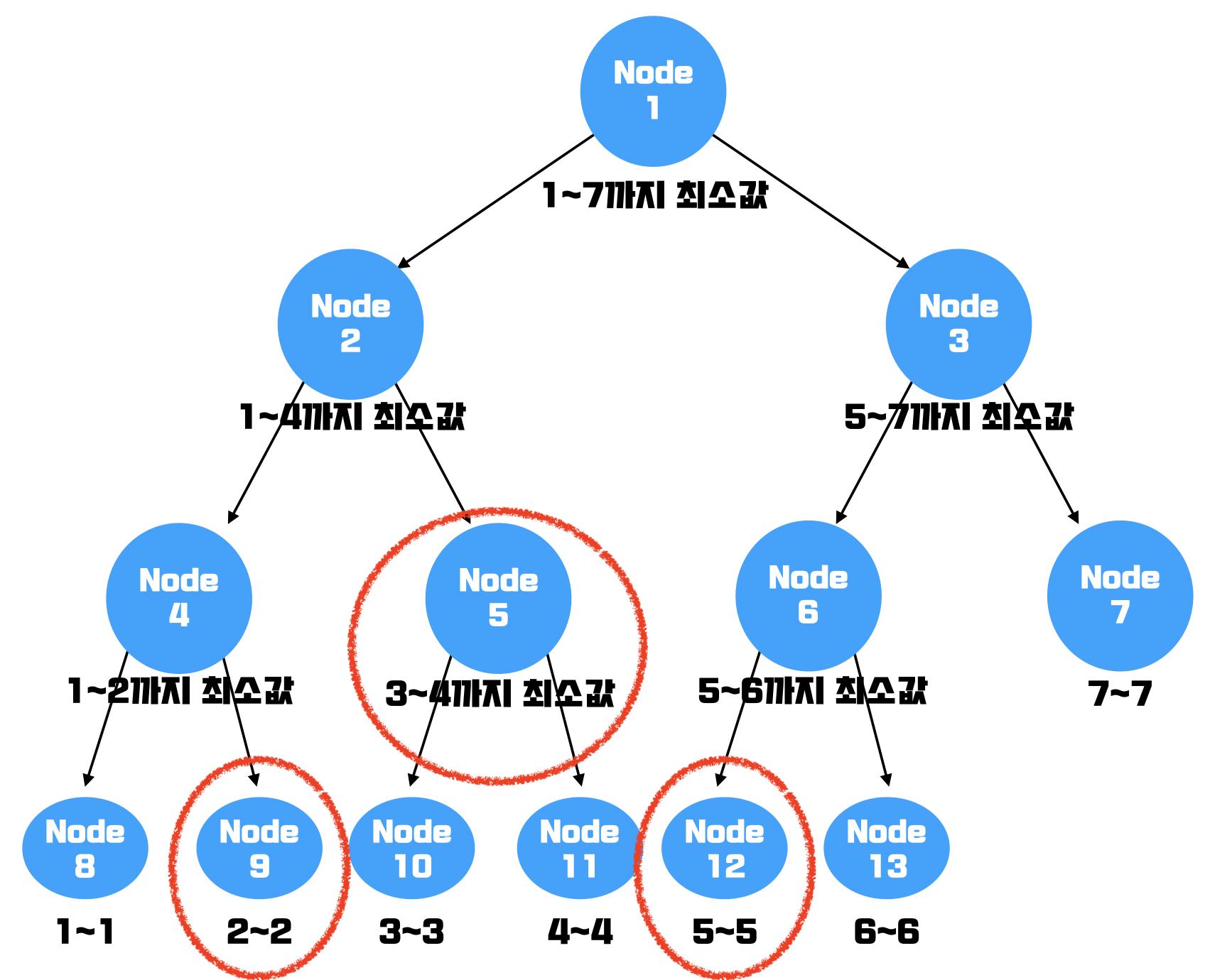이렇게 3개의 값만 조사하면 최소값을 얻을 수 있다! 이 때 발생하는 시간 복잡도는 $log(N)$ 이다. depth가 내려갈 수록 반씩 조사를 덜 할 수 있기 때문이다.

tree에 필요한 node 수

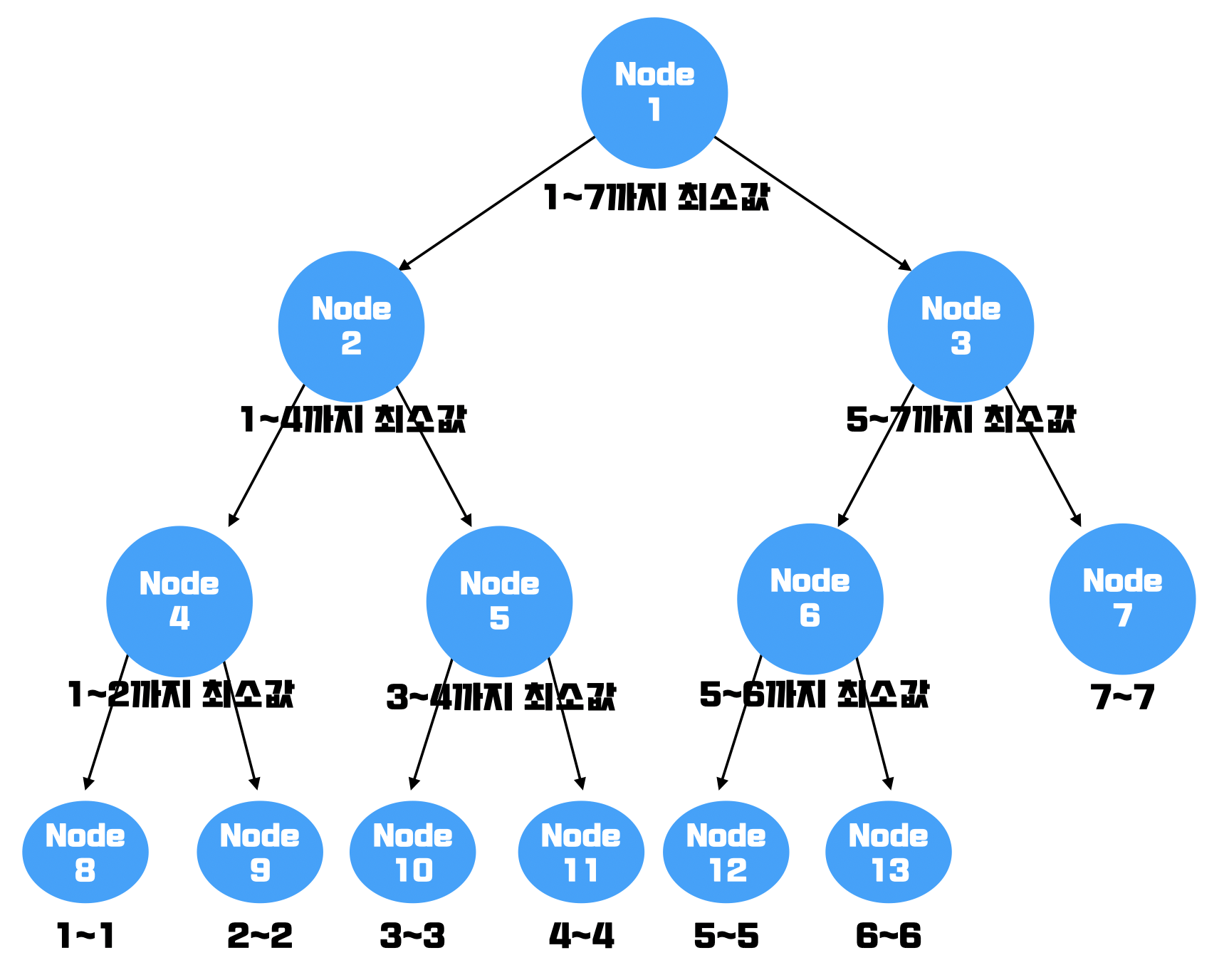
위 예시에서 총 7개의 원소를 넣기 위해 필요한 node의 개수는 총 13개 이다. 이 13개를 다 넣기 위해 필요한 트리의 깊이는 총 4이다. 이 값을 얻기 위한 수식은 다음과 같다.

$$\begin{gathered} depth=ceil(lo{g}_2(n))+1 \\ treeSize=2^{depth} \end{gathered}$$

보통의 tree는 input으로 들어오는 요소의 개수와 트리의 node번호가 일치하지만, 이 경우는 depth가 1개 추가되므로 1을 더해주어야 한다. 이것을 코드로 구현하면 다음과 같다.

h = ceil(log2(n))+1;
treeSize = (1 << h);

<<은 shift 연산자로, 2진 연산을 할 때, 자리수를 올려주는 역할을 한다.

init (초기화)

처음에 input을 받고서, 가장 먼저 해야하는 일은, input을 tree안에 넣는 것이다. 그런데 우리가 설계한 세그먼트 트리를 생각해보면, 이 친구는 아래 node가 결정된 뒤에 상위 노드가 결정될 수 있다. 재귀로 짜면 해결될 것이다.

void init(vector<int>& input, vector<int>& tree, int node, int start, int end){
    if (start == end) {
        tree[node] = input[start];
        return;
    }
    init(input, tree, 2*node, start, (start+end)/2);
    init(input, tree, 2*node+1, (start+end)/2+1, end);
    tree[node] = min(tree[2*node], tree[2*node+1]);
    return;
}

init 함수의 argument로는 input 벡터, tree 벡터, 내가 기록할 node의 index, 처음 node가 커버하게 될 index의 시작과 끝이 필요하다. 그 뒤로는 아까 트리 구조에서 본 왼쪽, 오른쪽 노드로 가는 함수 관계에 따라 init함수를 계속 수행하면 된다. 종료조건은, 그림에서 보았듯이 start와 end과 같아지는 지점에서 input에 start 해당하는 index의 값을 넣어준다.

find

저장된 자료구조에서 찾는 과정이다. 내가 찾으려고 하는 범위을 left, right 라 하고, 내가 처음에 탐색을 시작할 노드의 번호를 node, 그 노드가 커버하는 index의 범위를 start, end라 하자. tree의 가장 위부터 탐색을 시작할 때, 범위에 걸리는 녀석들만 비교의 대상이 되어야 한다. 이런 범위를 따져보면 총 3가지로 나눌 수 있다.

1. left, right 사이에 현재 노드의 커버범위가 들어온다.
   • 후보로 선정한다.
2. left, right 와 현재 노드의 커버범위가 전혀 겹치지 않는다.
   • 버린다.
3. 애매하게 걸친다.
   • 더 깊이 들어가서 조사한다.

이 과정을 구현하면 다음과 같다.

int findMin(vector<int>& tree, int node, int start, int end, int left, int right){
    if (left > end || right < start) {
        return INF;
    } else if (left <= start && end <= right){
        return tree[node];
    }
    int a = findMin(tree, 2*node, start, (start+end)/2, left, right);
    int b = findMin(tree, 2*node+1, (start+end)/2+1, end, left, right);
    return min(a, b);
}

Code

#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
 
const int INF = 1111111111;
 
void init(vector<int>& input, vector<int>& tree, int node, int start, int end){
    if (start == end) {
        tree[node] = input[start];
        return;
    }
    init(input, tree, 2*node, start, (start+end)/2);
    init(input, tree, 2*node+1, (start+end)/2+1, end);
    tree[node] = min(tree[2*node], tree[2*node+1]);
    return;
}
 
int findMin(vector<int>& tree, int node, int start, int end, int left, int right){
    if (left > end || right < start) {
        return INF;
    } else if (left <= start && end <= right){
        return tree[node];
    }
    int a = findMin(tree, 2*node, start, (start+end)/2, left, right);
    int b = findMin(tree, 2*node+1, (start+end)/2+1, end, left, right);
    return min(a, b);
}
 
 
int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);
 
    int n, m;
    cin >> n >> m;
    int h = int(ceil(log2(n)))+1;
    int treeSize = (1 << h);
    vector<int> tree(treeSize, INF);
    vector<int> a(n);
 
    for (int i = 0; i < n; i++) {
       cin >> a[i];
    }
    init(a, tree, 1, 0, n-1);
 
    for (int i = 0; i < m; i++) {
        int left, right;
        cin >> left >> right;
        cout << findMin(tree, 1, 0, n-1, left-1, right-1) << '\n';
    }
 
}

Reference

• 백준(10868번) - 최소값