골드4 : 수학 문제이다.
생각
문제 이름 부터 뭔가 마음에 들지 않았다. 풀이 방법은 바로 떠올랐는데 왜 요즘 이런게 구현이 안되는지… score가 최대공약수를 구하는 것이기 때문에 소인수 분해를 떠올릴 수 있고, 그러기 위해서는 소수를 구해야 한다. 그러니 소수를 구하는 가장 빠른 알고리즘인 에라토스 테네스의 체를 떠올릴 수 있다.
규칙의 이해
|8|24|9| |:|::|:| ||||
문제의 입력은 다음과 같다. 이 때 A,B를 정해서 문제에서 원하는 규칙에 따라 진행하는 것은, 각각의 수를 이루는 소수들 중 하나를 떼서 준다로 압축할 수 있다.
|A : 8→4|24|B : 9→18| |:------:|::|:-------:| ||||
이런 규칙을 가지고 문제에서 원하는 것을 구하기 위해서는 어떠한 상황이여야 하는지 생각해 보자.
최대 숫자
내가 가진 소인수의 개수를 서로에게 나눠주는 과정 속에서 최대한 잘 나눠가졌을 때, 공통된 숫자가 무엇이냐?
상당히 공리주의적 관점이다. 위의 조건을 만족하려면 각각이 가진 개수를 모두 파악한 후, 인원수로 나눈것이 모두가 고루고루 나누는 최종 숫자이다.
|8|24|9|1728|12| |:|::|:|:—:|::| ||||||
이 문제에서는 12라는 숫자가 답이 될 수 있겠다.
최소 이동 횟수
이제 답이 되는 후보를 알았다. 각각의 숫자를 그 숫자를 위해 움직여야 하는 횟수가 있을 것이다.
|8|24|9| |:|::|:| |||| |2|1|3|
- 8의 경우 12가 되기 위해서 2를 버리고 3을 얻어야 한다.
- 24의 경우 2를 버려야 한다.
- 9의 경우 2를 2개 얻고, 3을 버려야 한다.
총 6번의 움직임이 필요하지만, 이것은 하나의 행동이 2번씩 중복되어 나타났다. 이 것을 해소하기 위해서는 최종적으로 답을 내기 위해 2로 나누거나, 하나의 행동만을 제약해서 counting을 하면 된다. (답이 요구하는 개수보다 작을 경우만 센다)
구현
구현하기 위해 필요한 것을 생각해본다.
에라토스테네스의 체
에라토스테네스의 체는, 소수를 구하는 방법 중 가장 빠른 방법이다.
에라토스테네스의 체
- n까지의 소수는 범위 안에있는 소수를 가지고 구할 수 있다.
- 소인수 분해를 하면, 해당 수의 제곱근 보다 작은 소인수를 가지고 모든 약수를 구할 수 있다.
- 소수의 배수는 소수가 아니다.
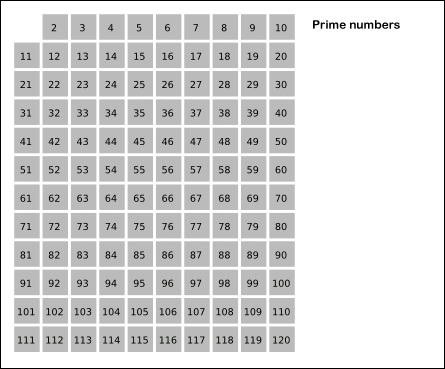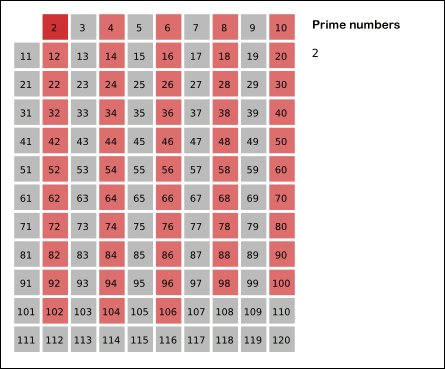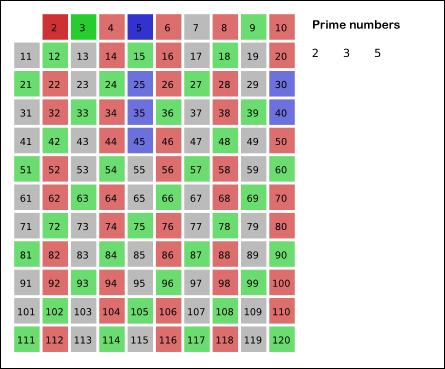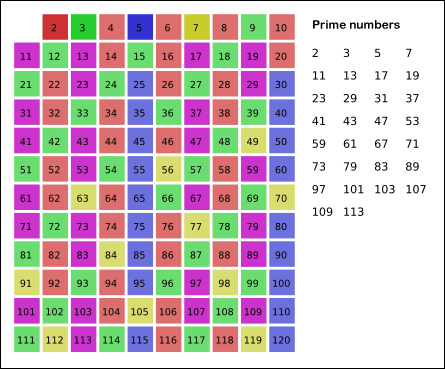
120까지의 소수를 구하기 위해서는 즉, 11보다 작은 수, 10까지의 수를 가지고 120까지의 소수를 구할 수 있다.
알고리즘
void SieveOfEratosthenes(){
for (int i = 2; i <= MAX; i++)
isPrime[i] = true;
for (int i = 2; i*i <= MAX; i++) {
if (!isPrime[i]) continue;
for (int j = i*i; j <= MAX; j+=i)
isPrime[j] = false;
}
}이 때, j를 부터 탐색하는 것에 주목하자. i 이전의 배수들은 그 전의 소수가 이미 걸렀기 때문이다. 해당 알고리즘의 시간 복잡도는 이다.
나머지 필요한 것들
- 에라토스테네스의 체를 통해 얻은 소수를 저장할 변수가 필요하다.
vector<int> primelist
- 각각의 입력되는 숫자에 대해 소인수 분해를 하여 담아둘 변수가 필요하다.
vector<vector<int>> input (n, vector<int> (primeNumberSize, 0))- n개의 숫자에 대해 1000000까지 발생하는 소수의 개수 만큼의 배열이 필요하다.
- j는 발생하는 소수를 오름차순으로 정렬했을 때의 index이다.
- 전체 소인수들의 개수를 저장할 변수가 필요하다.
vector<int> whole (primelist.size(), 0)
이제 해야 할 일은 순서도를 작성하는 것이다.
알고리즘
- 에라토스테네스의 체로 1000000까지의 소수를 구한다.
- 이 소수를 primelist에 저장한다.
- primelist의 개수만큼 whole, input 의 크기를 공간을 만든다.
- 각각의 input이 어떻게 소인수 분해되는지 구한다.
- 구하는 도중에 전체 배열에 추가한다.
- 다 구했다면 최종적으로 위에서 구한 방법으로 답을 구한다.
Code
#include <iostream>
#include <cmath>
#include <algorithm>
#include <functional>
#include <vector>
#include <set>
using namespace std;
typedef long long ll;
#define MAX 1000000
bool isPrime[MAX + 1];
int whole[MAX + 1];
//vector<int> primelist;
int N;
void SieveOfEratosthenes(){
for (int i = 2; i <= MAX; i++) isPrime[i] = true;
for (int i = 2; i*i <= MAX; i++) {
if (!isPrime[i]) continue;
// primelist.push_back(i); // 여기다 추가하면 1000 범위내의 소수만 들어간다..
for (int j = i*i; j <= MAX; j+=i) isPrime[j] = false;
}
}
int main(){
SieveOfEratosthenes();
cin >> N;
vector<int> primelist;
for (int i = 1; i <= MAX; i++) if (isPrime[i]) primelist.push_back(i);
vector<vector<int>> input(N, vector<int>(primelist.size(), 0));
for (int i = 0; i < N; i++) {
int num;
cin >> num;
for (int j = 0; j < primelist.size(); j++) {
if (num == 1) break;
while (num % primelist[j] == 0) {
num /= primelist[j];
whole[primelist[j]]++;
input[i][j]++;
}
}
}
int ans = 1, count = 0;
for (int i = 0; i < primelist.size(); i++) {
int currentWholePrimeCount = whole[primelist[i]]/N;
for (int j = 0; j < N; j++) {
if (currentWholePrimeCount > input[j][i])
count += (currentWholePrimeCount-input[j][i]);
}
ans *= pow(primelist[i], currentWholePrimeCount);
}
cout << ans << " " << count << '\n';
return 0;
}
//
// main.cpp
// test
//
// Created by 최완식 on 2021/03/15.
//
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <map>
using namespace std;
typedef long long ll;
bool isPrime[1001];
vector<int> Prime;
map<int, int> temp;
map<int, int> total;
vector<map<int, int>> eachNum;
void div(int a){
for (auto now: Prime) {
if (a%now == 0) {
temp[now]++;
total[now]++;
a /= now;
div(a);
return;
}
}
if (a != 1) {
total[a]++;
temp[a]++;
}
}
int main(){
for (int i = 2; i <= 1000; i++) {
if (isPrime[i]) {
continue;
}
Prime.push_back(i);
for (int j = i*i; j <= 1000; j+=i) {
isPrime[j] = true;
}
}
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int num;
cin >> num;
temp.clear();
div(num);
eachNum.push_back(temp);
}
ll ans = 1LL;
for (auto a: total){
total[a.first] = a.second/n;
ans *= pow(a.first, a.second/n);
}
int count = 0;
for (int i = 0; i < n; i++) {
for (auto a: total){
if (total[a.first] > eachNum[i][a.first]) {
count += total[a.first] - eachNum[i][a.first];
}
}
}
cout << ans << ' ' << count << endl;
return 0;
}