풀이
좀 어려울 수 있지만, 시간 초과가 나면 무언가 규칙이 있다는 생각을 해보자.
일단 찾을 수 있는 규칙은 다음과 같다.
- 최소공배수로 나눈 작은 모양이 반복되어 발생한다.
- 그렇다면 그 작은 모양에서 사라지는 사각형의 개수를 판단하여 최소공배수만큼 곱하면, 전체 사각형에서 지워지는 개수를 알 수 있다.
작은 사각형이란, w, h가 서로소인 경우를 말한다.
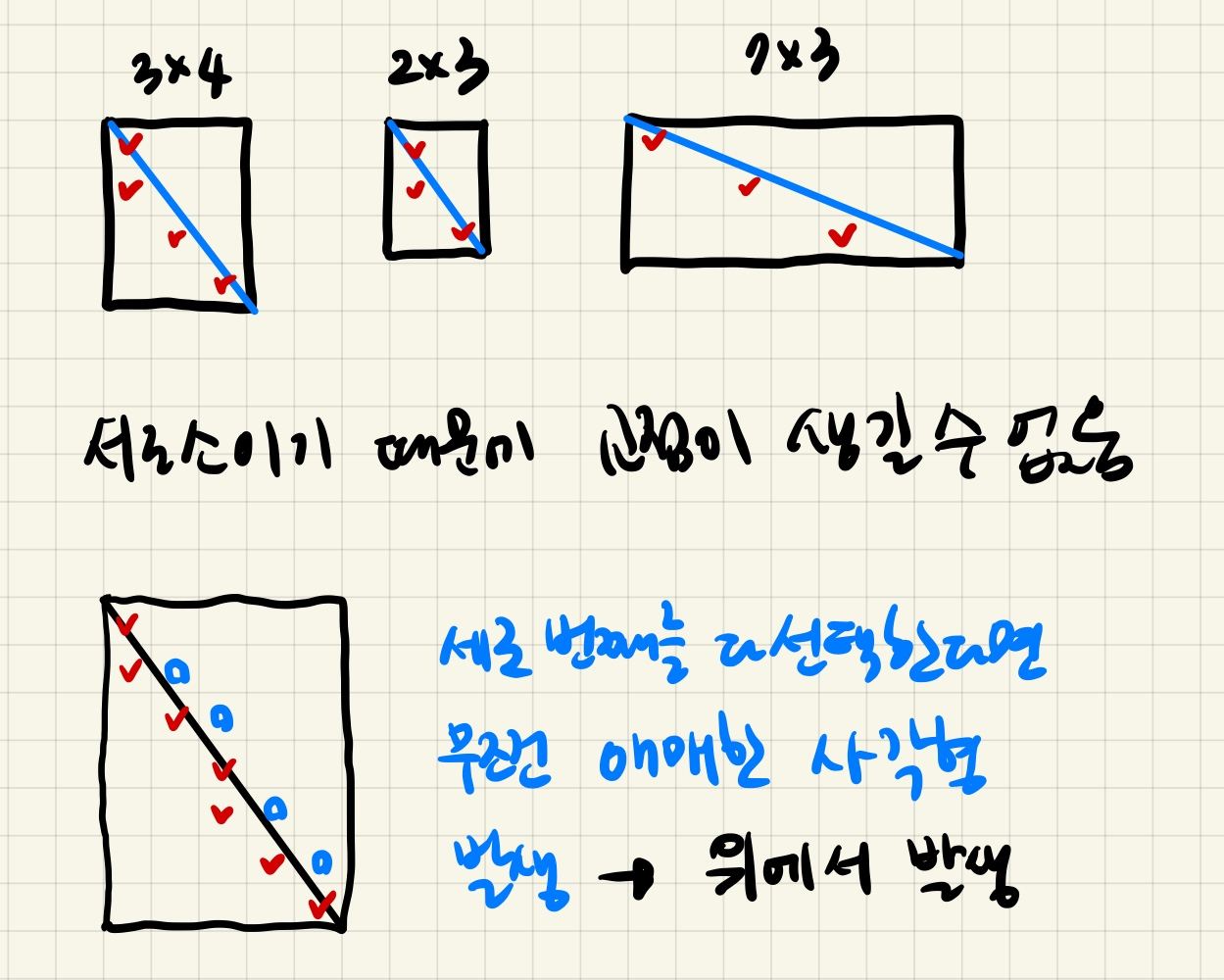
서로소인 상황만 생각해보자. 그랬을 경우 먼저 자명한 사실은, 선을 긋게되면, 적어도 h만큼의 개수의 사각형은 가려지게 된다. (반대로 w로 생각해도 무방하다) 이 때, 좌상부분 부터, h의 길이를 먼저 채운다는 생각으로 빨간색 동그라미를 칠하게 되면 위와 같다. 이 상황에서 그 다음으로 처리해야 하는 부분은 애매하게 지나가는 사각형이 몇개인지 세줘야 한다. 그런데 그 부분을 파란색 동그라미로 칠하다 보면 무조건 위에 칠해지게 되고, 그 개수가 w-1가 됨을 알 수 있다. (몇개 칠하지 않았지만 아래 그림을 보고 확인해보자.) 이 추론이 맞는지 생각해보면, 일단 서로소기 때문에 선을 그었을 때, 교점에 걸리는 경우는 있을 수 없다. 그런 경우 빨간색 동그라미를 치는 것과 같은 규칙을 적용하게 되면, 무조건적으로 특정 j열에 발생하는 애매한 사각형의 아래 부분에 빨간색 동그라미가 쳐지게 된다. 그럴 경우 위에 있는 애매한 사각형은 1개로 국한되는데, 그이유는 이전 j-1열에서 빨간색 동그라미가 쳐진 것이 이미 j열의 시작 부분을 커버하기 때문이다. j열의 나머지 부분은 높이를 담당하는 사각형을 세면서(빨간색 동그라미) 처리했기 때문에 j열에서 남는 애매한 사각형은 하나로 정해진다.
이런 흐름으로 이해를 완료했다면 코드는 간단하다.
Code
from collections import deque
def solution(bridge_length, weight, truck_weights):
answer = 0
t = 0
bridge_in = 0
truck = deque(truck_weights)
bridge = deque()
while truck or bridge: # 트럭이 남아 있으면
t += 1
# 다리에서 내리기
if bridge: # 다리에 타있으면 먼저 내려
a = bridge.popleft()
bridge_in -= a[0]
if t - a[1] < bridge_length: #들어온 시간이 아직 덜됐으면 다시 태우기
bridge.appendleft(a)
bridge_in += a[0]
# 태우기
if truck:
tr = truck.popleft()
if bridge_in+tr <= weight: # 이미 타있는 것과 지금꺼 추가해서 탈 수 있으면
bridge.append((tr, t)) # 다리 탑승
bridge_in += tr
else: # 탈수 없으면
truck.appendleft(tr) # 원상 복귀
answer = t
return answer